
【题目】在平面直角坐标系中,点A(a,0)、B(b,0)(a≠0),a、b满足![]() +b2+2bc+c2=0
+b2+2bc+c2=0
(1) 直接写出a与b的关系
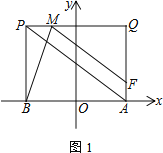
(2) 如图,将线段AB沿y轴的正方向平移m个单位得到线段PQ,点M在线段PQ上,QM=3MP,过M作MF∥PA交QA于点F,连接BM,BM平分∠PMF.若BM=![]() ,求m的值
,求m的值
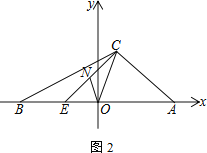
(3) 如图,点C在第一象限内,且满足CA=OA,点E在x轴上,AE=BC,连接CE,取CE的中点N,连接NO.若∠BCA=α,求∠NOC(用含α的代数式表示)
【答案】(1)a+b=0;(2)m=3;(3)∠NOC=90°-0.5ɑ
【解析】
(1)首先由题意,可得出![]() +
+![]() =0,进而可得出
=0,进而可得出![]() ;
;
(2)首先延长MF交x轴于F,得出MP,又因为MF∥PA,PM∥AH,得出四边形PMHA为平行四边形,进而得出AH和BH,又![]() ,即
,即![]() ,再根据BM平分∠PMF,即
,再根据BM平分∠PMF,即![]() ,得出
,得出![]() ,在Rt△PBA中,
,在Rt△PBA中,![]() ,即得出
,即得出
![]() ,即
,即![]() ,
,![]() ,在Rt△PBM中,
,在Rt△PBM中,![]() ,即
,即![]() ,将两个等式联立即可得出
,将两个等式联立即可得出![]() ;
;
(3)首先在OA上取一点F,使得OF=OE,连接CF,由BO=AO,EO=OF,BC=AE,得出BC=BF,进而得出∠BCF=∠BFC,又由N为CE的中点,即EO=OF,得出NO∥CF,进而得出∠NOC=∠OCF,又由∠BFC=∠FCA+∠FAC,∠BCO+∠OCF=∠BCF,得出∠FCA+∠FAC=∠BCO+∠OCF,又∠COA=∠BCO+∠CBO,将两式联立,得∠OCF=∠FCA+∠FAC-∠COA+∠CBO,又因为∠FAC+∠CBO=180°-α,得出∠OCF=180°-α-∠COA+∠FCA,又因为∠COA=∠OCF+∠FCA,得出∠OCF=90°-![]() ,即∠NOC=90°-
,即∠NOC=90°-![]() .
.
解:(1)由题意,得
![]() +b2+2bc+c2=0
+b2+2bc+c2=0
![]() +
+![]() =0
=0
∴![]()
∴![]()
(2)延长MF交x轴于F,如图所示
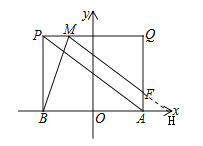
由题意得,P(b,m),Q(a,m)
又∵QM=3MP,
∴![]()
又∵MF∥PA,PM∥AH
∴四边形PMHA为平行四边形
∴![]() ,
,![]()
又![]() ,即
,即![]()
BM平分∠PMF,即![]()
∴![]() ,即
,即![]()
在Rt△PBA中,![]() ,
,![]() ,即
,即![]() ①
①
在Rt△PBM中,![]() ,即
,即
![]() ②
②
联立①②,解得
![]() .
.
(3)在OA上取一点F,使得OF=OE,连接CF,如图所示,
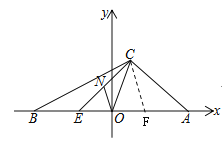
∵BO=AO,EO=OF,BC=AE,
∴BC=BF,
∴∠BCF=∠BFC,
又∵N为CE的中点,即EO=OF
∴NO∥CF
∴∠NOC=∠OCF
又∵∠BFC=∠FCA+∠FAC,∠BCO+∠OCF=∠BCF
∴∠FCA+∠FAC=∠BCO+∠OCF①
又∠COA=∠BCO+∠CBO②
①②联立,得∠OCF=∠FCA+∠FAC-∠COA+∠CBO
∵∠FAC+∠CBO=180°-α
∴∠OCF=180°-α-∠COA+∠FCA
又∵∠COA=∠OCF+∠FCA
∴∠OCF=90°-![]()
即∠NOC=90°-![]()


科目:初中数学 来源: 题型:
【题目】如图,菱形![]() 中,
中,![]() ,过点
,过点![]() 作
作![]() 交对角线
交对角线![]() 于点
于点![]() ,连接
,连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() .
.
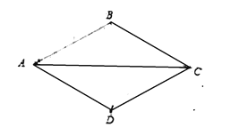
(1)请你根据题意补全图形;
(2)若![]() ,则菱形
,则菱形![]() 的面积为 .(直接写出答案)
的面积为 .(直接写出答案)
(3)请用等式表示线段![]() 、
、![]() 、
、![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1是由大小相同的小立方块搭成的几何体,请在图2的方格中画出从上面和左面看到的该几何体的形状图.(只需用2B铅笔将虚线化为实线)
(2)若要用大小相同的小立方块搭一个几何体,使得它从上面和左面看到的形状图与你在图2方格中所画的形状图相同,则搭这样的一个几何体最多需要 个小立方块.
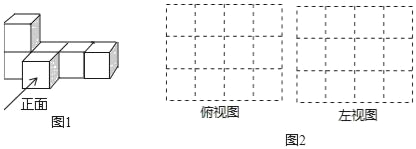
查看答案和解析>>
科目:初中数学 来源: 题型:
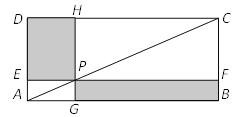
【题目】如图所示,点P在矩形ABCD的对角线AC上,且不与点A,C重合,过点P分别作边AB,AD的平行线,交两组对边于点E,F和点G,H.
(1)求证:△PHC≌△CFP;
(2)证明四边形 PEDH和四边形 PGBF都是矩形,并直接写出它们面积之间的关系。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列生活、生产现象中,可以用基本事实“两点确定一条直线”来解释的有( )
①用两颗钉子就可以把木条固定在墙上
②把笔尖看成一个点,当这个点运动时便得到一条线;
③把弯曲的公路改直,就能缩短路程;
④植树时,只要栽下两棵树,就可以把同一行树栽在同一条直线上。
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() >0)的对称轴与x轴交于点B,与直线l:
>0)的对称轴与x轴交于点B,与直线l:![]() 交于点C,点A是该二次函数图像与直线l在第二象限的交点,点D是抛物线的顶点,已知AC∶CO=1∶2,∠DOB=45°,△ACD的面积为2.
交于点C,点A是该二次函数图像与直线l在第二象限的交点,点D是抛物线的顶点,已知AC∶CO=1∶2,∠DOB=45°,△ACD的面积为2.
(1) 求抛物线的函数关系式;
(2) 若点P为抛物线对称轴上的一个点,且∠POC=45°,求点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图:在△ABC中,AC=3,BC=6,∠C=60![]() ;
;
(1)将△ABC绕着点C旋转,使点A落在直线BC上的点A′,点B落在B′,在下图中画出旋转后的△A′B′C.
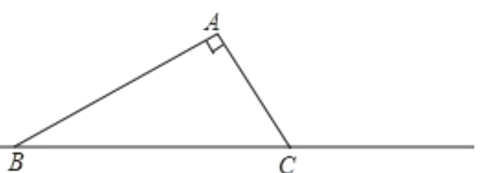
(2)直接写出A′B的长,A′B=___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索与发现
(1)正方形ABCD中有菱形PEFG,当它们的对角线重合,且点P与点B重合时(如图1),通过观察或测量,猜想线段AE与CG的数量关系,并证明你的猜想;
(2)当(1)中的菱形PEFG沿着正方形ABCD的对角线平移到如图2的位置时,猜想线段AE与CG的数量关系,只写出猜想不需证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】1955年,印度数学家卡普耶卡(![]() )研究了对四位自然数的一种变换:任给出四位数
)研究了对四位自然数的一种变换:任给出四位数![]() ,用
,用![]() 的四个数字由大到小重新排列成一个四位数
的四个数字由大到小重新排列成一个四位数![]() ,再减去它的反序数
,再减去它的反序数![]() (即将
(即将![]() 的四个数字由小到大排列,规定反序后若左边数字有0,则将0去掉运算,比如0001,计算时按1计算),得出数
的四个数字由小到大排列,规定反序后若左边数字有0,则将0去掉运算,比如0001,计算时按1计算),得出数![]() ,然后继续对
,然后继续对![]() 重复上述变换,得数
重复上述变换,得数![]() ,…,如此进行下去,卡普耶卡发现,无论
,…,如此进行下去,卡普耶卡发现,无论![]() 是多大的四位数,只要四个数字不全相同,最多进行
是多大的四位数,只要四个数字不全相同,最多进行![]() 次上述变换,就会出现变换前后相同的四位数
次上述变换,就会出现变换前后相同的四位数![]() ,这个数称为
,这个数称为![]() 变换的核.则四位数9631的
变换的核.则四位数9631的![]() 变换的核为______.
变换的核为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com