
【题目】1955年,印度数学家卡普耶卡(![]() )研究了对四位自然数的一种变换:任给出四位数
)研究了对四位自然数的一种变换:任给出四位数![]() ,用
,用![]() 的四个数字由大到小重新排列成一个四位数
的四个数字由大到小重新排列成一个四位数![]() ,再减去它的反序数
,再减去它的反序数![]() (即将
(即将![]() 的四个数字由小到大排列,规定反序后若左边数字有0,则将0去掉运算,比如0001,计算时按1计算),得出数
的四个数字由小到大排列,规定反序后若左边数字有0,则将0去掉运算,比如0001,计算时按1计算),得出数![]() ,然后继续对
,然后继续对![]() 重复上述变换,得数
重复上述变换,得数![]() ,…,如此进行下去,卡普耶卡发现,无论
,…,如此进行下去,卡普耶卡发现,无论![]() 是多大的四位数,只要四个数字不全相同,最多进行
是多大的四位数,只要四个数字不全相同,最多进行![]() 次上述变换,就会出现变换前后相同的四位数
次上述变换,就会出现变换前后相同的四位数![]() ,这个数称为
,这个数称为![]() 变换的核.则四位数9631的
变换的核.则四位数9631的![]() 变换的核为______.
变换的核为______.
【答案】6174
【解析】
用9631的四个数字由大到小排列成一个四位数9631.则9631-1369=8262,用8262的四个数字由大到小重新排列成一个四位数8622.则8622-2268=6354,类似地进行上述变换,可知5次变换之后,此时开始停在一个数6174上.
解:用9631的四个数字由大到小排列成一个四位数9631.则9631-1369=8262,
用8262的四个数字由大到小重新排列成一个四位数8622.则8622-2268=6354,
用6354的四个数字由大到小重新排列成一个四位数6543.则6543-3456=3087,
用3087的四个数字由大到小重新排列成一个四位数8730.则8730-378=8352,
用8352的四个数字由大到小重新排列成一个四位数8532.则8532-2358=6174,
用6174的四个数字由大到小重新排列成一个四位数7641.则7641-1467=6174…
可知7次变换之后,四位数最后都会停在一个确定的数6174上.
故答案为:6174.


科目:初中数学 来源: 题型:
【题目】某小区准备新建![]() 个停车位,以解决小区停车难的问题。已知新建
个停车位,以解决小区停车难的问题。已知新建![]() 个地上停车位和
个地上停车位和![]() 个地下停车位共需
个地下停车位共需![]() 万元:新建
万元:新建![]() 个地上停车位和
个地上停车位和![]() 个地下停车位共需
个地下停车位共需![]() 万元,
万元,
(1)该小区新建![]() 个地上停车位和
个地上停车位和![]() 个地下停车位各需多少万元?
个地下停车位各需多少万元?
(2)若该小区新建车位的投资金额超过![]() 万元而不超过
万元而不超过![]() 万元,问共有几种建造方案?
万元,问共有几种建造方案?
(3)对(2)中的几种建造方案中,哪种方案的投资最少?并求出最少投资金额.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】六年级(1)班从学校出发,乘大巴车去农场进行实践活动,之后返回学校(大巴车行驶速度不变),下图反映的是大巴车行驶路程与时间之间的关系。请同学们观察图象,进行数据分析,求大巴车离开学校多少小时时,大巴车与农场相距![]() 。
。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动课上,老师准备了若千个如图1的三种纸片,![]() 种纸片是边长为
种纸片是边长为![]() 的正方形,
的正方形,![]() 种纸片是边长为
种纸片是边长为![]() 的正方形,
的正方形,![]() 种纸片是长为
种纸片是长为![]() ,宽为
,宽为![]() 的长方形.并用
的长方形.并用![]() 种纸片一张,
种纸片一张,![]() 种纸片一张,
种纸片一张,![]() 种纸片两张拼成如图2的大正方形.
种纸片两张拼成如图2的大正方形.

(1)请用两种不同的方法求图2大正方形的面积:方法1: ,方法2: _;
(2)观察图2,请你写出代数式:![]() 之间的等量关系 ;
之间的等量关系 ;
(3)根据(2)题中的等量关系,解决如下问题:①已知:![]() ,求
,求![]() 的值;②已知
的值;②已知![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
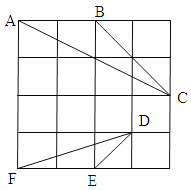
【题目】如图,在4×4的正方格中,△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.
(1)填空:∠ABC , BC= ;
(2)判断△ABC与△DEF是否相似,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若规定两数a、b通过“※”运算,得到4ab,即a※b=4ab,例如2※6=4×2×6=48
(1)求3※5的值;
(2)求x※x+2※x-2※4=0中x的值;
(3)若无论x是什么数,总有a※x=x,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜生产基地的气温较低时,用装有恒温系统的大棚栽培一种新品种蔬菜.如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度y (℃)与时间x(h)之间的函数关系,其中线段AB、BC表示恒温系统开启阶段,双曲线的一部分CD表示恒温系统关闭阶段.
请根据图中信息解答下列问题:
(1)求这天的温度y与时间x(0≤x≤24)的函数关系式;
(2)求恒温系统设定的恒定温度;
(3)若大棚内的温度低于10℃时,蔬菜会受到伤害.问这天内,恒温系统最多可以关闭多少小时,才能使蔬菜避免受到伤害?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大坝横截面的迎水坡AD的坡比为4:3,背水坡BC的坡比为1:2,大坝高DE=50m,坝顶宽CD=30m.则AD=_______m,大坝的周长是__________m.(坡比:垂直高度与水平距离之比,运算结果保留根号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com