
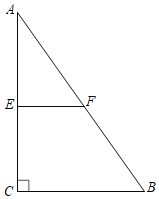
【题目】如图,在直角三角形ABC中,∠C=90°,∠B=60°,AB=8cm,E、F分别为边AC、AB的中点.
(1)求∠A的度数;
(2)求EF和AE的长.
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】某学校抽查了某班级某月10天的用电量,数据如下表:
用电量/度 | 8 | 9 | 10 | 13 | 14 | 15 |
天数 | 1 | 1 | 2 | 3 | 1 | 2 |
(1)这10天用电量的众数是______度,中位数是______度;
(2)求这个班级平均每天的用电量;
(3)该校共有20个班级,该月共计30天,试估计该校该月总的用电量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】预习了“线段、射线、直线”一节的内容后,乐乐所在的小组,对如图展开了激烈的讨论,下列说法不正确的是( )
![]()
A. 直线AB与直线BA是同一条直线
B. 射线OA与射线AB是同一条射线
C. 射线OA与射线OB是同一条射线
D. 线段AB与线段BA是同一条线段
查看答案和解析>>
科目:初中数学 来源: 题型:
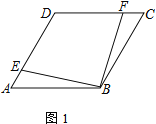
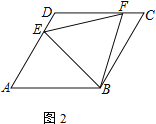
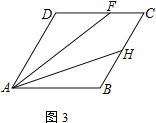
【题目】四边形ABCD为菱形,点E在边AD上,点F在边CD上
(1) 若AE=CF,求证:EB=BF
(2) 若AD=4,DE=CF,且△EFB为等边三角形,求四边形DEBF的面积
(3) 若∠DAB=60°,点H在边BC上,且BH=HC=2.若∠DFA=2∠HAB,直接写出CF的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() >0)的对称轴与x轴交于点B,与直线l:
>0)的对称轴与x轴交于点B,与直线l:![]() 交于点C,点A是该二次函数图像与直线l在第二象限的交点,点D是抛物线的顶点,已知AC∶CO=1∶2,∠DOB=45°,△ACD的面积为2.
交于点C,点A是该二次函数图像与直线l在第二象限的交点,点D是抛物线的顶点,已知AC∶CO=1∶2,∠DOB=45°,△ACD的面积为2.
(1) 求抛物线的函数关系式;
(2) 若点P为抛物线对称轴上的一个点,且∠POC=45°,求点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
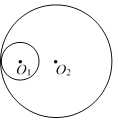
【题目】如图,半径为1的圆O1与半径为3的圆O2相内切,如果半径为2的圆与圆O1和圆O2都相切,那么这样的圆的个数是 ( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一块矩形纸片ABCD,AB=8,AD=6.将纸片折叠,使得AD边落在AB边上,折痕为AE,再将△AED沿DE向右翻折,AE与BC的交点为F,则CF的长为________

查看答案和解析>>
科目:初中数学 来源: 题型:
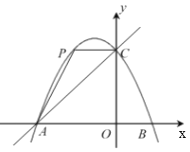
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于点A、B,与y轴交于点C,直线y=x+4经过点A、C,点P为抛物线上位于直线AC上方的一个动点.
与x轴交于点A、B,与y轴交于点C,直线y=x+4经过点A、C,点P为抛物线上位于直线AC上方的一个动点.
(1)求抛物线的表达式;
(2)如图,当CP//AO时,求∠PAC的正切值;
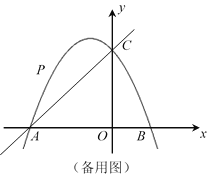
(3)当以AP、AO为邻边的平行四边形第四个顶点恰好也在抛物线上时,求出此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表所示:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法中,错误的是( )
A. 抛物线于x轴的一个交点坐标为(﹣2,0)
B. 抛物线与y轴的交点坐标为(0,6)
C. 抛物线的对称轴是直线x=0
D. 抛物线在对称轴左侧部分是上升的
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com