练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

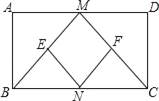
    【题目】如图，在矩形ABCD中，M，N分别是AD，BC的中点，E，F分别是线段BM，CM的中点，若AB=8，AD=12，则四边形ENFM的周长是多少？

    【答案】20

    【解析】分析：根据M是边AD的中点，得AM=DM=6，根据勾股定理得出BM=CM=10，再根据E、F分别是线段BM、CM的中点，即可得出EM=FM=5，再根据N是边BC的中点，得出EM=FN，EN=FM，从而得出四边形ENFM的周长．

    详解：∵M、N分别是边AD、BC的中点，AB=8，AD=12，

    ∴AM=DM=6，

    ∵四边形ABCD为矩形，

    ∴∠A=∠D=90°，

    ∴BM=CM=10，

    ∵E、F分别是线段BM、CM的中点，

    ∴EM=FM=5，

    ∴EN，FN都是△BCM的中位线，

    ∴EN=FN=5，

    ∴四边形ENFM的周长为5+5+5+5=20．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】计算

    （1）﹣24﹣11015

    （2）﹣3×（﹣）÷

    （3）（﹣）÷

    （4）1÷（﹣1）+0÷4﹣5×0.1×（﹣2）3

    （5）（﹣1）2009+（﹣2）3+2×（﹣3）2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

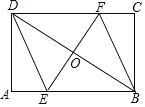
    【题目】如图，矩形ABCD中，AB=6，BC=4，过对角线BD中点O的直线分别交AB，CD边于点E，F．

    （1）求证：四边形BEDF是平行四边形；

    （2）当四边形BEDF是菱形时，求EF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

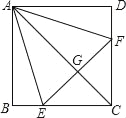
    【题目】如图，正方形ABCD中，点E，F分别在BC，CD上，三角形AEF是等边三角形，连接AC交EF于G，下列结论：①BE=DF，②AG=2GC，③BE+DF=EF，④S△CEF=2S△ABE正确的有_____（只填序号）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，中，，，是上一点，且，过点分别作，，垂足分别是，下列结论：①；②是的中点；③垂直平分；④；其中正确的个数为（ ）

    A. 1个B. 2个C. 3个D. 4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

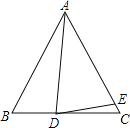
    【题目】已知中，，为边上一点，为上一点，，设，

    （1）若，，则__________；__________；若，，则__________；__________；

    （2）由此猜想与的关系，并证明.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

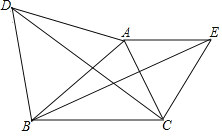
    【题目】如图，已知△ABC ，分别以AB 、AC 为边在△ABC 的外部作等边三角形ABD和等边三角形ACE联结DC 、BE 试说明DCBE的理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，菱形中，，过点作交对角线于点，连接，取的中点，连接.

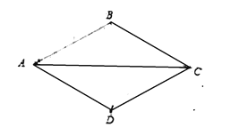
    （1）请你根据题意补全图形；

    （2）若，则菱形的面积为 .（直接写出答案）

    （3）请用等式表示线段、、之间的数量关系，并证明.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

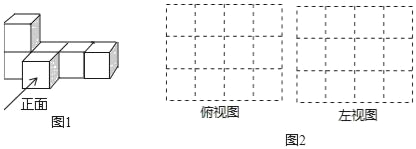
    【题目】（1）如图1是由大小相同的小立方块搭成的几何体，请在图2的方格中画出从上面和左面看到的该几何体的形状图．（只需用2B铅笔将虚线化为实线）

    （2）若要用大小相同的小立方块搭一个几何体，使得它从上面和左面看到的形状图与你在图2方格中所画的形状图相同，则搭这样的一个几何体最多需要　 　个小立方块．

    查看答案和解析>>

    同步练习册答案