(1)证明:∵方程①有两个相等的实数根,
∴△
1=0,
即n-1≠0,m
2-4(n-1)=0,
m
2=4(n-1).
因为m
2≥0,n≠1.
∴m
2=4(n-1)>0,n>1.
方程②中,△
2=(-2m)
2-4m
2(-m
2-2n
2+3)=4m
2(1+m
2+2n
2-3)=4m
2(m
2+2n
2-2).
将m
2=4n-4代入,得△
2=4m
2(2n
2+4n-6)=8m
2(n+3)(n-1).
∵m
2>0,n>1.
∴△
2>0,
∴方程②有两个不相等的实数根.
(2)解:∵方程①有两个相等的实数根,
∴两根都是-

,
则-
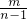
=-1,

=

,
解得n=5,m=4.
代入方程②得16y
2-8y-16-50+3=0.
解得y
1=-

,y
2=

.
分析:(1)方程①有两个相等的实数根,则n-1≠0,△
1=0,可得m
2=4n-4>0,代入方程②的判别式△
2=8m
2(n+3)(n-1)>0.
(2)于方程①两根相等,都是-

,由根与系数的关系,列出m与n的方程组,求出m与n的值,代入方程②,求出其根.
点评:(1)一元二次方程根的情况与判别式△的关系:
①△>0?方程有两个不相等的实数根;
②△=0?方程有两个相等的实数根;
③△<0?方程没有实数根.
(2)一元二次方程根与系数的关系:x
l+x
2=-

,x
l•x
2=

.

 ,求方程②的根.
,求方程②的根. ,
,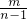 =-1,
=-1, =
= ,
, ,y2=
,y2= .
. ,由根与系数的关系,列出m与n的方程组,求出m与n的值,代入方程②,求出其根.
,由根与系数的关系,列出m与n的方程组,求出m与n的值,代入方程②,求出其根. ,xl•x2=
,xl•x2= .
. 

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案