
销售单价 (元∕件) (元∕件) | …… | 30 | 40 | 50 | 60 | …… |
每天销售量 (件) (件) | …… | 500 | 400 | 300 | 200 | …… |
 、
、 的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想
的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想 与
与 的函数关系,并求出函数关系式;
的函数关系,并求出函数关系式; 
 =-10
=-10 +800(2)当销售单价定为50元∕件时,工艺厂试销该工艺品每天获得的利润最大,最大利润是9000元(3)45元
+800(2)当销售单价定为50元∕件时,工艺厂试销该工艺品每天获得的利润最大,最大利润是9000元(3)45元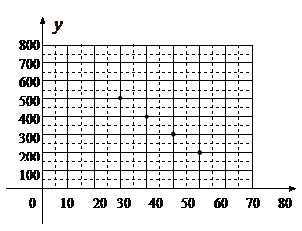
 与
与 是一次函数关系,····· 3分
是一次函数关系,····· 3分 =
= 
 +
+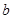 (k≠0)
(k≠0) 解得
解得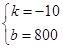 ……5分
……5分  =-10
=-10 +800 ……6分
+800 ……6分 -20)(-10
-20)(-10 +800)······················· 8分
+800)······················· 8分
 +1000
+1000 -16000
-16000 -50)
-50)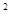 +9000 ························ 9分
+9000 ························ 9分 =50时,W有最大值9000.
=50时,W有最大值9000. -50)
-50)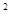 +9000,当
+9000,当 ≤45时,
≤45时, 值的增大而增大, ······················· 11分
值的增大而增大, ······················· 11分 -50)
-50)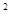 +9000,销售单价最高不能超过45元/件,W随x的增大而减小,故销售单价定为45元∕件时,工艺厂试销该工艺品每天获得的利润最大
+9000,销售单价最高不能超过45元/件,W随x的增大而减小,故销售单价定为45元∕件时,工艺厂试销该工艺品每天获得的利润最大

 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.y=2(x+1)2+3 | B.y=2(x-1)2-3 |
| C.y=2(x+1)2-3 | D.y=2(x-1)2+3 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 ⑤a+b+c>m(am+b)+c,(m>1的实数),其中正确的结论有( )
⑤a+b+c>m(am+b)+c,(m>1的实数),其中正确的结论有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.1个 | B.2个 | C.3个 | D.4个 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.1个 | B.2个 | C.3个 | D.4个 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com