
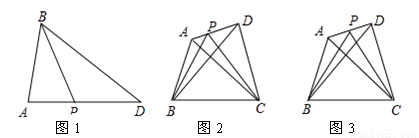
点P是△ABD中AD边上一点,
1.如图1,当P为AD中点时,则有S△ABP= S△ABD;
2.如图2,在四边形ABCD中,P是AD边上任意一点,△PBC的面积为 ,△ABC的面积为
,△ABC的面积为 ,△DBC的面积为
,△DBC的面积为 。
。
①当AP= AD时,如图3,试探究
AD时,如图3,试探究 、
、 、
、 之间的关系?写出求解过程;
之间的关系?写出求解过程;
②一般地,当AP= AD(n表示正整数)时,试探究
AD(n表示正整数)时,试探究 、
、 、
、 之间的关系?写出求解过程。
之间的关系?写出求解过程。

1.S△ABP=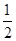 S△ABD;
S△ABD;
2.①当AP= AD时(如图②):
AD时(如图②):
∵AP= AD,△ABP和△ABD的高相等,
AD,△ABP和△ABD的高相等,
∴S△ABP= S△ABD。
S△ABD。
∵PD=AD-AP= AD,△CDP和△CDA的高相等,
AD,△CDP和△CDA的高相等,
∴S△CDP= S△CDA。
S△CDA。
∴S△PBC=S四边形ABCD-S△ABP-S△CDP
=S四边形ABCD- S△ABD-
S△ABD- S△CDA
S△CDA
=S四边形ABCD- (S四边形ABCD-S△DBC)-
(S四边形ABCD-S△DBC)- (S四边形ABCD-S△ABC)
(S四边形ABCD-S△ABC)
= S△DBC+
S△DBC+ S△ABC。
S△ABC。
②S△PBC= S△DBC+
S△DBC+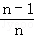 S△ABC;
S△ABC;
∵AP= AD,△ABP和△ABD的高相等,
AD,△ABP和△ABD的高相等,
∴S△ABP= S△ABD。
S△ABD。
又∵PD=AD-AP=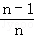 AD,△CDP和△CDA的高相等,
AD,△CDP和△CDA的高相等,
∴S△CDP=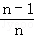 S△CDA
S△CDA
∴S△PBC=S四边形ABCD-S△ABP-S△CDP
=S四边形ABCD- S△ABD-
S△ABD-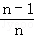 S△CDA
S△CDA
=S四边形ABCD- (S四边形ABCD-S△DBC)-
(S四边形ABCD-S△DBC)-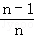 (S四边形ABCD-S△ABC)
(S四边形ABCD-S△ABC)
= S△DBC+
S△DBC+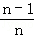 S△ABC。
S△ABC。
∴S△PBC= S△DBC+
S△DBC+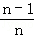 S△ABC
S△ABC
【解析】(1)因为△ABP和△ABD的高相等,所以S△ABP=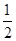 S△ABD
S△ABD
(2)①当AP= AD时,△ABP和△ABD的高相等,所以S△ABP=
AD时,△ABP和△ABD的高相等,所以S△ABP= S△ABD,同理S△CDP=
S△ABD,同理S△CDP= S△CDA,通过
S△CDA,通过
S△PBC=S四边形ABCD-S△ABP-S△CDP得出结论
②与①证法相同


科目:初中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| m |
| n |
| m |
| n |
查看答案和解析>>
科目:初中数学 来源:2011-2012学年北京市101中学下学期七年级期中考试数学试卷(带解析) 题型:解答题
点P是△ABD中AD边上一点,
【小题1】如图1,当P为AD中点时,则有S△ABP= S△ABD;
【小题2】如图2,在四边形ABCD中,P是AD边上任意一点,△PBC的面积为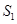 ,△ABC的面积为
,△ABC的面积为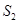 ,△DBC的面积为
,△DBC的面积为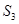 。
。
①当AP=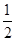 AD时,如图3,试探究
AD时,如图3,试探究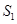 、
、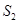 、
、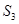 之间的关系?写出求解过程;
之间的关系?写出求解过程;
②一般地,当AP=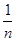 AD(n表示正整数)时,试探究
AD(n表示正整数)时,试探究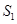 、
、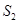 、
、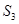 之间的关系?写出求解过程。
之间的关系?写出求解过程。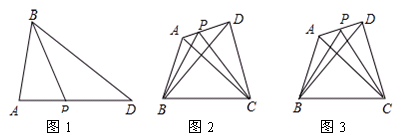
查看答案和解析>>
科目:初中数学 来源:2011年安徽省中考说明数学检测卷(二)(解析版) 题型:解答题
 S△BDP,如图2,在四边形ABCD中,P是AD边上任意一点,探究:
S△BDP,如图2,在四边形ABCD中,P是AD边上任意一点,探究: AD时,如图3,△PBC与△ABC和△DBC的面积之间有什么关系?写出求解过程;
AD时,如图3,△PBC与△ABC和△DBC的面积之间有什么关系?写出求解过程; AD时,探究S△PBC与S△ABC和S△DBC之间的关系,写出求解过程;
AD时,探究S△PBC与S△ABC和S△DBC之间的关系,写出求解过程;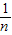 AD(n表示正整数)时,探究S△PBC与S△ABC和S△DBC之间的关系,写出求解过程;
AD(n表示正整数)时,探究S△PBC与S△ABC和S△DBC之间的关系,写出求解过程;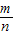 AD(0≤
AD(0≤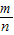 ≤1)时,直接写出S△PBC与S△ABC和S△DBC之间的关系.
≤1)时,直接写出S△PBC与S△ABC和S△DBC之间的关系.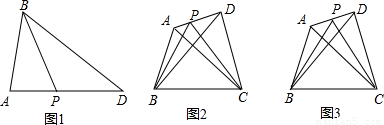
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com