
分析 (1)根据非负数的性质求得a、b的值;从而可以求得点A、B表示的数;
(2)先求出x的值,再由PA+PB=PC,可得出点P对应的数;
(3)根据A,B,C的运动情况即可确定AB,BC的变化情况,即可确定AB-BC的值.
解答 解:(1)∵|a+2|+(b-1)2=0,
∴a+2=0,b-1=0,
解得,a=-2,b=1,
即点A表示的数是-2,点B表示的数是1;
故线段AB的长度是3.
故答案是:-2;1;3;
(2)存在.
由方程2x-1=$\frac{1}{2}$x+2,得x=$\frac{8}{3}$,
所以点C在数轴上对应的数为$\frac{8}{3}$.
设点P对应的数为m,
若点P在点A和点B之间,m-(-2)+1-m=$\frac{8}{3}$-m,解得m=-$\frac{1}{3}$;
若点P在点A右边,-2-m+1-m=$\frac{8}{3}$-m,解得m=-$\frac{11}{3}$.
所以P对应的数为-$\frac{1}{3}$或-$\frac{11}{3}$.
(3)AB-BC=(5t+3)-(5t+$\frac{5}{3}$)=$\frac{4}{3}$,
所以AB-BC的值是否随着时间t的变化而不变.
点评 本题考查数轴、一元一次方程的解,解题的关键是明确题意,找出所求问题需要的条件,利用数相结合的思想解答问题.


科目:初中数学 来源: 题型:解答题
 已知:如图,AB为⊙O的直径,点P是⊙O上不与A,B重合的一个动点,延长PA到C,使AC=AP,点D为⊙O上一点,且满足AD∥PB,射线CD交PB延长线于点E.
已知:如图,AB为⊙O的直径,点P是⊙O上不与A,B重合的一个动点,延长PA到C,使AC=AP,点D为⊙O上一点,且满足AD∥PB,射线CD交PB延长线于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
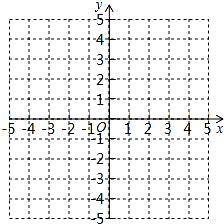 在平面直角坐标系中,A(5,4)、B(4,2)、C(1,0).
在平面直角坐标系中,A(5,4)、B(4,2)、C(1,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
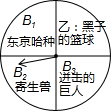 周助是个动漫迷,妈妈用周助喜欢的动漫设计了下面的游戏:用如图被平均分成4份的转盘,转动转盘,转盘静止后,指针指向一个动漫名.若所指的动漫名不在文化部动漫黑名单内,则周助每天可以看一集动漫;否则,周助三天才可以看一集动漫.(注:B系列在文化部动漫黑名单内)
周助是个动漫迷,妈妈用周助喜欢的动漫设计了下面的游戏:用如图被平均分成4份的转盘,转动转盘,转盘静止后,指针指向一个动漫名.若所指的动漫名不在文化部动漫黑名单内,则周助每天可以看一集动漫;否则,周助三天才可以看一集动漫.(注:B系列在文化部动漫黑名单内)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com