
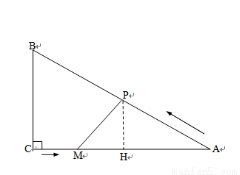
(本小题满分12分) 如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M从点C出发,以每秒1cm的速度沿CA向终点A移动,同时动点P从点A出发,以每秒2cm的速度沿AB向终点B移动,连接PM,设移动时间为t(s)(0<t<2.5).
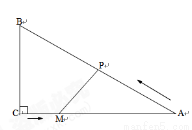
(1)当AP=AM时,求t的值.
(2)设四边形BPMC的面积为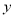 (cm),求y与t之间的函数关系式;
(cm),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使四边形BPMC的面积是Rt△ABC面积的 ?若存在,求出相应t的值,若不存在,说明理由;
?若存在,求出相应t的值,若不存在,说明理由;
(4)是否存在某一时刻t,使以M,P,A为顶点的三角形与△ABC相似?若存在,求出相应t的值;若不存在,说明理由.
(1)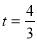 ;(2)y =
;(2)y =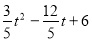 ;(3)t=2;(4)
;(3)t=2;(4)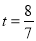 或
或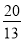 .
.
【解析】
试题分析:(1)因为AM=4-t,AP=2t,所以当AP=AM时,则4-t= 2t,解方程得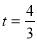 ;(2)过点P作PH⊥AC于点H,根据
;(2)过点P作PH⊥AC于点H,根据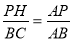 得PH=
得PH=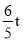 ,利用
,利用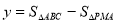 可求出函数关系式y =
可求出函数关系式y =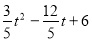 ;(3)假设存在某一时刻t,使四边形BPMC的面积是Rt△ABC面积的
;(3)假设存在某一时刻t,使四边形BPMC的面积是Rt△ABC面积的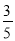 ,则
,则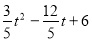 =
=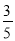 ×6,然后解方程即可;(4)分△AMP∽△ABC和△APM∽△ABC两种情况讨论.
×6,然后解方程即可;(4)分△AMP∽△ABC和△APM∽△ABC两种情况讨论.
试题解析:【解析】
(1)如图,
∵在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.
∴根据勾股定理,得AB=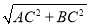 =5cm.
=5cm.
AM=4-t,AP=2t
当AP=AM时,则
4-t= 2t, ∴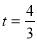
当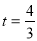 时, AP=AM 3分
时, AP=AM 3分
过点P作PH⊥AC于点H,则PH∥BC,
∴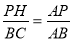 ,即
,即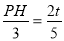 ∴PH=
∴PH=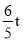 .
.
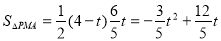
∴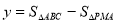 =6-(
=6-(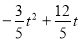 )
)
y =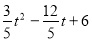 7分
7分
(3)假设存在某一时刻t,使四边形BPMC的面积是Rt△ABC面积的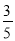 ,则
,则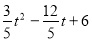 =
=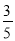 ×6,解方程得
×6,解方程得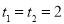 ,因为(0<t<2.5),所以当t=2时,四边形BPMC的面积是Rt△ABC面积的
,因为(0<t<2.5),所以当t=2时,四边形BPMC的面积是Rt△ABC面积的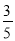 ; 9分
; 9分
(4)分两种情况讨论,当 △AMP∽△ABC时 所以
所以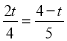 解得
解得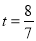 ,当△APM∽△ABC时,
,当△APM∽△ABC时,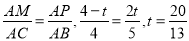 ,所以当
,所以当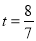 或
或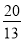 时,以M,P,A为顶点的三角形与△ABC相似 12分.
时,以M,P,A为顶点的三角形与△ABC相似 12分.
考点:1.勾股定理;2.等腰三角形的性质;3.相似三角形的判定与性质;4.函数与几何知识.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源:2014-2015学年云南省九年级上学期第一轮测试数学试卷(解析版) 题型:选择题
若关于x的方程(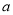 -1)x
-1)x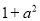 =1是一元二次方程,则
=1是一元二次方程,则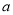 的值是( )
的值是( )
A、0 B、-1 C、±1 D、1
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,是我们学过的用直尺画平行线的方法示意图,画图原理是( )
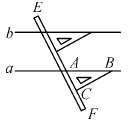
A.同位角相等,两直线平行 B.内错角相等,两直线平行
C.两直线平行,同位角相等 D.两直线平行,内错角相等
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省滕州市九年级下学期学业水平模拟考试1数学试卷(解析版) 题型:填空题
PM2.5是指大气中宣径小予或等于2.5微米的颗粒物,也称为可入肺颗粒物.2.5微米等于0.0000025米,把0.0000025用科学记数法表示为_____.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省滕州市九年级下学期学业水平模拟考试1数学试卷(解析版) 题型:解答题
如图是根据某班40名同学一周的体育锻炼情况绘制的条形统计图,那么该班40名同学一周体育锻炼时间的众数、中位数分别是
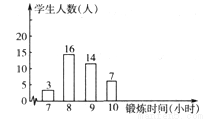
A.16,10.5 B.8,9 C.16,8.5 D.8,8.5
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级上学期期末调研数学试卷(解析版) 题型:解答题
(本小题满分8分)如图所示,反比例函数y1的图象经过点A(3,2),解答下列问题:
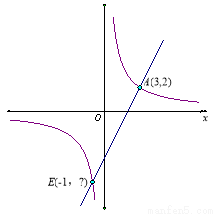
(1)求y1的函数关系式;
(2)过y1上任意一点B向x轴,y轴作垂线,交两坐标轴于C,D两点,求矩形OCBD的面积;
(3)过点A的一次函数y2与反比例函数y1的另一个交点E的横坐标为-1,求y2的关系式;
(4)通过图象回答当x取何值时,y1>y2;
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级上学期期末调研数学试卷(解析版) 题型:填空题
如图,点B1在反比例函数y=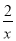 (x>0)的图象上,过点B1分别作x轴和y轴的垂线,垂足为C1和A,得到第一个矩形AOC1B1,点C1的坐标为(1,0);取x轴上一点C2(
(x>0)的图象上,过点B1分别作x轴和y轴的垂线,垂足为C1和A,得到第一个矩形AOC1B1,点C1的坐标为(1,0);取x轴上一点C2( ,0),过点C2作x轴的垂线交反比例函数图象于点B2,过B2作线段B2 A1⊥B1C1,,交B1C1于点A1,得到第二个矩形A1C1C2B2;依次在x轴上取点C3(2,0),C4(
,0),过点C2作x轴的垂线交反比例函数图象于点B2,过B2作线段B2 A1⊥B1C1,,交B1C1于点A1,得到第二个矩形A1C1C2B2;依次在x轴上取点C3(2,0),C4(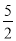 ,0) 按此规律作矩形,则第10个矩形A9C9C10B10的面积为 .
,0) 按此规律作矩形,则第10个矩形A9C9C10B10的面积为 .

查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省如皋市九年级12月阶段测试数学试卷(解析版) 题型:解答题
已知:如图,菱形ABCD中,对角线AC,BD相交于点O,且AC=12cm,BD=16cm.点P从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,直线EF从点D出发,沿DB方向匀速运动,速度为1cm/s,EF⊥BD,且与AD,BD,CD分别交于点E,Q,F;当直线EF停止运动时,点P也停止运动.连接PF,设运动时间为t(s)(0<t<8).解答下列问题:
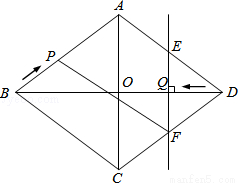
(1)当t为何值时,四边形APFD是平行四边形?
(2)设四边形APFE的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使S四边形APFE:S菱形ABCD=17:40?若存在,求出t的值,并求出此时P,E两点间的距离;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年黑龙江省大庆市林甸县九年级上学期期末检测数学试卷(解析版) 题型:解答题
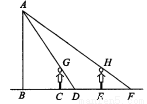
如图,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1米,继续往前走3米到达E处时,测得影子EF的长为2米,已知王华的身高是1.5米,那么路灯的高度AB等于多少呢?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com