
已知:如图,菱形ABCD中,对角线AC,BD相交于点O,且AC=12cm,BD=16cm.点P从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,直线EF从点D出发,沿DB方向匀速运动,速度为1cm/s,EF⊥BD,且与AD,BD,CD分别交于点E,Q,F;当直线EF停止运动时,点P也停止运动.连接PF,设运动时间为t(s)(0<t<8).解答下列问题:
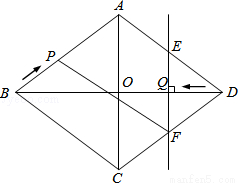
(1)当t为何值时,四边形APFD是平行四边形?
(2)设四边形APFE的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使S四边形APFE:S菱形ABCD=17:40?若存在,求出t的值,并求出此时P,E两点间的距离;若不存在,请说明理由.
(1) 当t=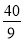 s时,四边形APFD是平行四边形.(2)y=-
s时,四边形APFD是平行四边形.(2)y=-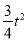 +
+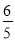 t+48.(3)
t+48.(3) 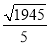 cm.
cm.
【解析】
试题分析:(1))由四边形ABCD是菱形,OA=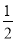 AC,OB=
AC,OB=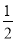 BD.在Rt△AOB中,运用勾股定理求出AB=10.再由△DFQ∽△DCO.得出
BD.在Rt△AOB中,运用勾股定理求出AB=10.再由△DFQ∽△DCO.得出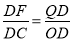 .求出DF.由AP=DF.求出t.
.求出DF.由AP=DF.求出t.
(2)过点C作CG⊥AB于点G,由S菱形ABCD=ABCG=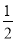 ACBD,求出CG.据S梯形APFD=
ACBD,求出CG.据S梯形APFD=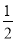 (AP+DF)CG.S△EFD=
(AP+DF)CG.S△EFD=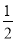 EFQD.得出y与t之间的函数关系式;
EFQD.得出y与t之间的函数关系式;
(3)过点C作CG⊥AB于点G,由S菱形ABCD=ABCG,求出CG,由S四边形APFE:S菱形ABCD=17:40,求出t,再由△PBN∽△ABO,求得PN,BN,据线段关系求出EM,PM再由勾股定理求出PE.
试题解析:(1)∵四边形ABCD是菱形,
∴AB∥CD,AC⊥BD,OA=OC=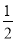 AC=6, OB=OD=
AC=6, OB=OD=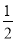 BD=8.
BD=8.
在Rt△AOB中,AB=10
∵EF⊥BD,
∴∠FQD=∠COD=90°.
又∵∠FDQ=∠CDO,
∴△DFQ∽△DCO.
∴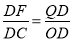 .即
.即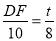
∴DF=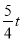
∵四边形APFD是平行四边形,
∴AP=DF.
即10-t=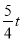
解这个方程,得t=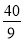 .
.
∴当t=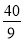 s时,四边形APFD是平行四边形.
s时,四边形APFD是平行四边形.
(2)如图,过点C作CG⊥AB于点G,
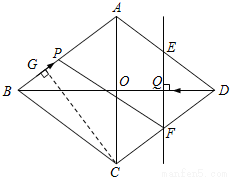
∵S菱形ABCD=ABCG=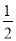 ACBD,
ACBD,
即10CG=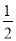 ×12×16,
×12×16,
∴CG=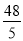
∴S梯形APFD=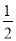 (AP+DF)CG
(AP+DF)CG
=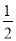 (10-t+
(10-t+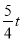 )
)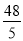
=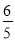 t+48.
t+48.
∵△DFQ∽△DCO,
∴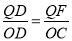
即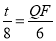
∴QF=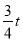 .
.
同理,EQ=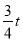
∴EF=QF+EQ=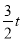 .
.
∴S△EFD=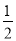 EFQD=
EFQD=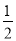 ×
×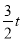 ×t=
×t=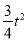 .
.
∴y=(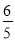 t+48)-
t+48)-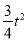 =-
=-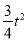 +
+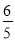 t+48.
t+48.
(3)如图,过点P作PM⊥EF于点M,PN⊥BD于点N,
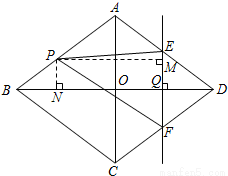
若S四边形APFE:S菱形ABCD=17:40,
则-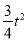 +
+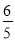 t+48=
t+48=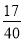 ×96,
×96,
即5t2-8t-48=0,
解这个方程,得t1=4,t2=-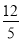 (舍去)
(舍去)
过点P作PM⊥EF于点M,PN⊥BD于点N,
当t=4时,
∵△PBN∽△ABO,
∴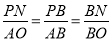
即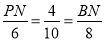
∴PN=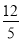 ,BN=
,BN=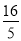
∴EM=EQ-MQ=3-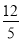 =
=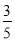
PM=BD-BN-DQ=16-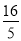 -4=
-4=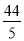
在Rt△PME中,
PE=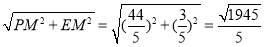 cm.
cm.
考点:1.四边形综合题;2.相似三角形的性质.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源:2014-2015学年山东省新泰市九年级上学期学业水平模拟数学试卷(解析版) 题型:选择题
如图,在□ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE,EC的长度分别为( )
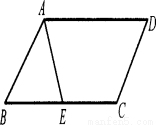
A.2和3 B.3和2 C.4和1 D.1和4
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级上学期期末调研数学试卷(解析版) 题型:解答题
(本小题满分12分) 如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M从点C出发,以每秒1cm的速度沿CA向终点A移动,同时动点P从点A出发,以每秒2cm的速度沿AB向终点B移动,连接PM,设移动时间为t(s)(0<t<2.5).
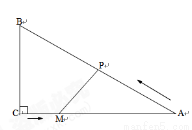
(1)当AP=AM时,求t的值.
(2)设四边形BPMC的面积为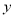 (cm),求y与t之间的函数关系式;
(cm),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使四边形BPMC的面积是Rt△ABC面积的 ?若存在,求出相应t的值,若不存在,说明理由;
?若存在,求出相应t的值,若不存在,说明理由;
(4)是否存在某一时刻t,使以M,P,A为顶点的三角形与△ABC相似?若存在,求出相应t的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级上学期期末调研数学试卷(解析版) 题型:填空题
一个不透明的袋中装有若干个红球,为了估计袋中红球的个数,小文在袋中放入10个白球(每个球除颜色外其余都与红球相同).摇匀后每次随机从袋中摸出一个球,记下颜色后放回袋中,通过大量重复摸球试验后发现,摸到白球的频率是 ,则袋中红球约为 _____个.
,则袋中红球约为 _____个.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级上学期期末调研数学试卷(解析版) 题型:选择题
在一个不透明的袋子中装有4个除颜色外完全相同的小球,其中白球1个,黄球1个,红球2个,摸出一个球不放回,再摸出一个球,两次都摸到红球的概率是( )
A.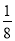 B.
B.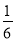 C.
C.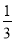 D.
D.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省如皋市九年级12月阶段测试数学试卷(解析版) 题型:解答题
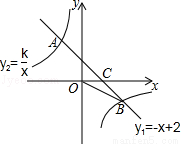
如图,一次函数y1=﹣x+2的图象与反比例函数y2=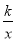 的图象相交于A,B两点,与x轴相交于点C.已知tan∠BOC=
的图象相交于A,B两点,与x轴相交于点C.已知tan∠BOC=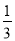 ,点B的坐标为(m,n).
,点B的坐标为(m,n).
(1)求反比例函数的解析式;
(2)请直接写出当x<m时,y2的取值范围.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省如皋市九年级12月阶段测试数学试卷(解析版) 题型:填空题
在平面直角坐标系 中,已知一次函数
中,已知一次函数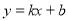 的图像经过点P(1,1),与
的图像经过点P(1,1),与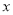 轴交于点A,与
轴交于点A,与 轴交于点B,且
轴交于点B,且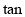 ∠ABO=3,那么A点的坐标是 .
∠ABO=3,那么A点的坐标是 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省如皋市九年级12月阶段测试数学试卷(解析版) 题型:选择题
用半径为6的半圆围成一个圆锥的侧面,则圆锥的底面半径等于( )
A.3 B.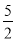 C.2 D.
C.2 D.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省长汀县城区三校九年级12月联考数学试卷(解析版) 题型:解答题
(12分)某商场将进价为30元的书包以40元售出, 平均每月能售出600个,调查表明:这种书包的售价每上涨1元,其销售量就减少10个。
(1)请写出每月售出书包的利润y元与每个书包涨价x元间的函数关系式;
(2)设每月的利润为10000的利润是否为该月最大利润?如果是,请说明理由;如果不是,请求出最大利润,并指出此时书包的售价应定为多少元。
(3)请分析售价在什么范围内商家所获利润不低于6000元。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com