
 如图,在Rt△ABC和Rt△CDE中,AB与CE相交于点F,∠ACB=∠E=90°,∠A=30°,∠D=45°,BC=6$\sqrt{2}$,求CF的长.
如图,在Rt△ABC和Rt△CDE中,AB与CE相交于点F,∠ACB=∠E=90°,∠A=30°,∠D=45°,BC=6$\sqrt{2}$,求CF的长. 分析 过F作FM⊥BC于M,则∠FMC=∠FMB=90°,解直角三角形求出FM=$\frac{\sqrt{2}}{2}$CF,BM=$\frac{FM}{tan60°}$=$\frac{\sqrt{6}}{6}$CF,根据BC=CM+BM=6$\sqrt{2}$求出即可.
解答 解:过F作FM⊥BC于M,则∠FMC=∠FMB=90°,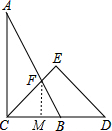
∵∠ECD=45°,
∴∠CFM=45°=∠FCM,
∴CM=FM=CF×sin45°=$\frac{\sqrt{2}}{2}$CF,
∵∠A=30°,∠ACB=90°,
∴∠FBM=60°,
∴BM=$\frac{FM}{tan60°}$=$\frac{\sqrt{2}}{2}$CF×$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{6}}{6}$CF,
∵BC=CM+BM=6$\sqrt{2}$,
∴$\frac{\sqrt{2}}{2}$CF+$\frac{\sqrt{6}}{6}$CF=6$\sqrt{2}$,
解得:CF=18-6$\sqrt{3}$.
点评 本题考查了解直角三角形的应用,首先根据实际问题建立三角形模型,本题的三角形不是直角三角形,还要添加辅助线构造直角三角形,然后利用解决三角形知识解决问题.


科目:初中数学 来源: 题型:选择题
 某学校准备从甲、乙、丙三位候选人中选拔一人做学生会主席,100名学生代表对这三位候选人进行民主评议投票推荐(每位代表只能投1票,没有弃权票),甲、乙、丙三位候选人得票情况统计结果如扇形图所示,那么甲得的票数是( )
某学校准备从甲、乙、丙三位候选人中选拔一人做学生会主席,100名学生代表对这三位候选人进行民主评议投票推荐(每位代表只能投1票,没有弃权票),甲、乙、丙三位候选人得票情况统计结果如扇形图所示,那么甲得的票数是( )| A. | 45 | B. | 35 | C. | 34 | D. | 31 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知平行四边形ABCD中,E为AD中点,点G在BC边上,且∠1=∠2.
如图,已知平行四边形ABCD中,E为AD中点,点G在BC边上,且∠1=∠2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com