
 某厂家在甲、乙两家商场销售同一商品所获利润分别为y甲,y乙(单位:元),y甲,y乙与销售数量x(单位:件)的函数关系如图所示,请根据图象解决下列问题:
某厂家在甲、乙两家商场销售同一商品所获利润分别为y甲,y乙(单位:元),y甲,y乙与销售数量x(单位:件)的函数关系如图所示,请根据图象解决下列问题:分析 (1)根据图象找出点的坐标,利用待定系数法即可求出一次函数关系式;
(2)设分配给乙商场x件,则分配给甲商场(1200-x)件,根据y甲+y乙=1080即可得出关于x的一元一次方程,解之即可得出结论.
解答 解:(1)设y甲=kx(k≠0),y乙=mx+n,
将(600,480)代入y甲=kx,
480=600k,解得:k=0.8,
∴y甲与x的函数关系式为y甲=0.8x;
当0≤x≤200时,将(0,0)、(200,400)代入y乙=mx+n中,
$\left\{\begin{array}{l}{n=0}\\{200m+n=400}\end{array}\right.$,解得:$\left\{\begin{array}{l}{m=2}\\{n=0}\end{array}\right.$,
∴此时y乙=2x;
当200≤x时,将(200,400)、(600,480)代入y乙=mx+n中,
$\left\{\begin{array}{l}{200m+n=400}\\{600m+n=480}\end{array}\right.$,解得:$\left\{\begin{array}{l}{m=0.2}\\{n=360}\end{array}\right.$,
∴此时y乙=0.2x+360.
∴y乙与x的函数关系式为y乙=$\left\{\begin{array}{l}{2x(0≤x≤200)}\\{0.2x+360(x≥200)}\end{array}\right.$.
(2)设分配给乙商场x件,则分配给甲商场(1200-x)件,
当0≤x≤200时,有0.8×(1200-x)+2x=1080,
解得:x=100,
此时1200-x=1100;
当x≥200时,有0.8×(1200-x)+0.2x+360=1080,
解得:x=400,
此时1200-x=800.
答:厂家分配该商品给甲商场1100件乙商场100件或甲商场800件乙商场400件时,厂家可获得总利润的1080元.
点评 本题考查了一次函数的应用、待定系数法求一次函数解析式以及一元一次方程的应用,解题的关键是:(1)根据点的坐标利用待定系数法求出一次函数关系式;(2)令y甲+y乙=1080找出关于x的一元一次方程.


科目:初中数学 来源: 题型:选择题
| A. | 若a2=b2,则a=b | |
| B. | 等角的补角相等 | |
| C. | n边形的外角和为(n-2)•180° | |
| D. | 三角形的一个外角等于它的两个内角的和 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
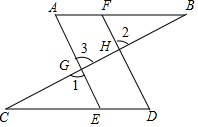 完成下面的推理过程:
完成下面的推理过程:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
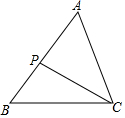 如图,在△ABC中,P是边AB上一点,连结CP,下面条件中能使△ACP∽△ABC的条件有( )个.
如图,在△ABC中,P是边AB上一点,连结CP,下面条件中能使△ACP∽△ABC的条件有( )个.| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 50.30千克 | B. | 49.51千克 | C. | 50.70千克 | D. | 49.80千克 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
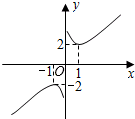 已知正比例函数y1=x,反比例函数y2=$\frac{1}{x}$,由y1,y2构成一个新函数y=x+$\frac{1}{x}$,其图象如图所示,(因其图象似双钩,我们称之为“双钩函数”)给出下列几个命题:
已知正比例函数y1=x,反比例函数y2=$\frac{1}{x}$,由y1,y2构成一个新函数y=x+$\frac{1}{x}$,其图象如图所示,(因其图象似双钩,我们称之为“双钩函数”)给出下列几个命题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com