
如图,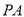 、
、 分别切⊙
分别切⊙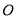 于点
于点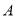 、
、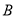 ,点
,点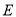 是⊙
是⊙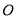 上一点,且
上一点,且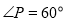 ,则
,则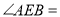 度;若PA=4,则AO= .
度;若PA=4,则AO= .
120;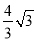 .
.
【解析】
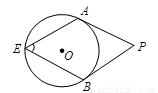
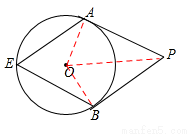
试题分析:连接OA,BO,OP,由圆周角定理知可知∠AOB=2∠E,PA、PB分别切⊙O于点A、B,利用切线的性质可知∠OAP=∠OBP=90°,根据四边形内角和可求得∠AOB=180°-∠P=180°-60°=120°,从而得出∠AEB的度数;再由切线长定理得出∠APO=30°,根据三角函数求解即可:
如图,连接OA,BO,OP,
∵PA、PB分别切⊙O,∴∠OAP=∠OBP=90°.
∵∠P=60°,∴∠AOB=180°-∠P=180°-60°=120°.
∵∠AOB=2∠E=120°,∴∠AEB=60°.
∵∠P=60°,∴∠APO=30°.
∴Rt△AOP中,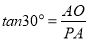 ,
,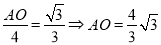 .
.
考点:1.圆周角定理;2.切线的性质;3.多边形的内角和定理;4. 锐角三角函数定义;5.特殊角的三角函数值.


 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源:2013-2014学年江苏省无锡市九年级3月阶段测试数学试卷(解析版) 题型:选择题
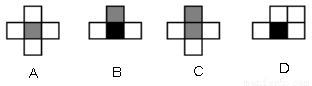
如果用□表示1个立方体,用 表示两个立方体叠加,用■表示三个立方体叠加,那么下面右图由7个立方体叠成的几何体,从正前方观察,可画出的平面图形是( )
表示两个立方体叠加,用■表示三个立方体叠加,那么下面右图由7个立方体叠成的几何体,从正前方观察,可画出的平面图形是( )

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省张家港市九年级5月网上阅卷适应性考试数学试卷(解析版) 题型:解答题
为了倡导“节约用水,从我做起”的活动,某市政府决定对市直机关500户家庭的用水情况作一次调查,调查小组随机抽查了其中100户家庭一年的月平均用水量(单位:吨).并将调查结果制成了如图所示的条形统计图.

(1)求这100个样本数据的平均数、众数和中位数;
(2)根据样本数据,估计该市直机关500户家庭中月平均用水量不超过12吨的约有多少户?
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省张家港市九年级5月网上阅卷适应性考试数学试卷(解析版) 题型:选择题
已知x2-y2=14,x-y=2,则x+y等于
A.6 B.7 C.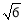 D.
D.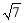
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省常州市九年级中考一模数学试卷(解析版) 题型:解答题
为了解某校九年级学生体育测试成绩情况,现从中随机抽取部分学生的体育成绩统计如下,其中右侧扇形统计图中的圆心角α为36°.
体育成绩统计表
体育成绩(分) | 人数(人) | 百分比(%) |
26 | 8 | 16 |
27 |
| 24 |
28 | 15 |
|
29 |
|
|
30 |
|
|

根据上面提供的信息,回答下列问题:
⑴ 填写表格中所缺数据,并写出样本容量与这些学生体育成绩的中位数;
⑵ 已知该校九年级共有500名学生,如果体育成绩达28分以上(含28分)为优秀,请估计该校九年级学生体育成绩达到优秀的人数.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省常州市九年级中考一模数学试卷(解析版) 题型:选择题
如图所示的几何体中,俯视图形状相同的是( )

A.①④ B.②④ C.①②④ D.②③④
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省太仓市九年级5月学科教学质量调研数学试卷(解析版) 题型:解答题
如图①,已知二次函数的解析式是y=ax2+bx(a>0),顶点为A(1,-1).
(1)a= ;
(2)若点P在对称轴右侧的二次函数图像上运动,连结OP,交对称轴于点B,点B关于顶点A的对称点为C,连接PC、OC,求证:∠PCB=∠OCB;
(3)如图②,将抛物线沿直线y=-x作n次平移(n为正整数,n≤12),顶点分别为A1,A2,…,An,横坐标依次为1,2,…,n,各抛物线的对称轴与x轴的交点分别为D1,D2,…,Dn,以线段AnDn为边向右作正方形AnDnEnFn,是否存在点Fn恰好落在其中的一个抛物线上,若存在,求出所有满足条件的正方形边长;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com