
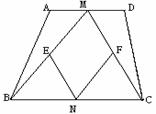
如图,在等腰梯形ABCD中,M、N分别为AD、BC的中点,E、F分别为BM、CM的中点。
(1)求证:△ABM≌△CDM;
(2)判断并证明四边形MENF是何种特殊的四边形;
‚当等腰梯形ABCD的高h与底边BC满足怎样的数量关系时,四边形MENF是正方形?(直接写出结论,不需要证明).
科目:初中数学 来源: 题型:
下列命题中 ①对角线相等且互相垂直的四边形是菱形;②若 ,那么sinɑ>cosɑ③一正多边形的一个外角是45°,则此图形是正八边形;④若式子
,那么sinɑ>cosɑ③一正多边形的一个外角是45°,则此图形是正八边形;④若式子 有意义,则x>1;⑤在反比例函数
有意义,则x>1;⑤在反比例函数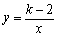 中,若x>0 时,y随x的增大而增大,则k的取值范围是k>2;其中假命题有( )
中,若x>0 时,y随x的增大而增大,则k的取值范围是k>2;其中假命题有( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
函数y=x2+bx+c与y=kx的图象如图所示,有以下结论:①b2﹣4c>0;②b+c+1=0;③2b+c<﹣2;④当1<x<3时,x2+(b﹣k)x+c<0.其中正确的是( )【根据2013年德州中考改编】
A①④ B②③ C③④ D①②

查看答案和解析>>
科目:初中数学 来源: 题型:
在学习掷硬币的概率时,老师说:“掷一枚质地均匀的硬币,正面朝上的概率是 ”,小明做了下列三个模拟实验来验证。
”,小明做了下列三个模拟实验来验证。
①取一枚新硬币,在桌面上进行抛掷,计算正面朝上的次数与总次数的比值。
②把一个质地均匀的圆形转盘平均分成偶数份,并依次标上奇数和偶数,转动转盘,
计算指针落在奇数区域的次数与总次数的比值。
③将一个圆形纸板放在水平的桌面上,纸板正中间放一个圆锥(如右图),从圆锥的正上方往下撒米粒,计算其中一半纸板上的米粒数与纸板上总米粒数的比值。上面的实验中,合理的有( )
A.0个 B.1个 C.2个 D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=1米;上部CDG是等边三角形,固定点E为AB的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆.
(1)当MN和AB之间的距离为0.5米时,求此时△EMN的面积;
(2)设MN与AB之间的距离为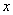 米,试将△EMN的面积S(平方米)表示成关于x的函数;
米,试将△EMN的面积S(平方米)表示成关于x的函数;
(3)请你探究△EMN的面积S(平方米)有无最大值,若有,请求出这个最大值;若没有,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com