
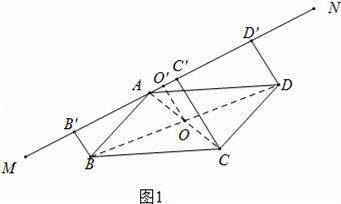
已知:如图,直线MN经过▱ABCD的顶点A,BB′⊥MN,CC′⊥MN,DD′⊥MN,B′、C′、D′是垂足.
(1)求证:CC′=BB′+DD′.
(2)现将直线MN向上或向下平移,请分别按下面要求画出示意图,写出这时四条垂线段AA′、BB′、CC′、DD′之间的等量关系式.并简要说明证明思路.
(ⅰ)使点A、B、C、D都在直线MN的同一侧,这时 ;
(ⅱ)使A点在MN的一侧,点B、C、D在另一侧,这时 ;
(ⅲ)使点A、B在MN的一侧,点C、D在另一侧,这时 .


【考点】平行四边形的性质;全等三角形的判定与性质.
【分析】(1)如图1中,连接AC、BD交于点O,作OO′⊥MN于O′,利用三角形中位线定理以及梯形中位线定理即可证明.
(2)(ⅰ)如图2中,结论AA′+CC′=BB′+DD,连接AC、BD交于点O,作OO′⊥MN于OO′,利用梯形中位线定理可以证明AA′+CC′=BB′+DD.
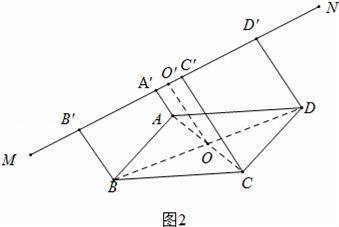
(ⅱ)如图3中,结论CC′﹣AA′=BB′+DD,连接AC、BD交于点O,作OO′⊥MN于OO′,延长A′O交CC′于E,只要证明CC′﹣AA′=2OO′.BB′+DD′=2OO′即可.
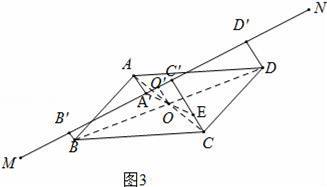
(ⅲ)如图4中,结论CC′﹣AA′=DD′﹣BB,连接AC、BD交于点O,作OO′⊥MN于OO′,证明方法类似.
【解答】(1)证明:如图1中,连接AC、BD交于点O,作OO′⊥MN于O′.
∵四边形ABCD是平行四边形,
∴AO=OC,BO=BD,
∵BB′⊥MN.OO′⊥MN,CC′⊥MN,DD′⊥MN,
∴BB′∥OO′∥CC′∥DD′,
∴B′O′=O′D′,AO′=O′C′,
∴CC′=2OO′,BB′+DD′=2OO′,
∴CC′=BB′+DD′.
(2)(ⅰ)当点A、B、C、D都在直线MN的同一侧,
如图2中,连接AC、BD交于点O,作OO′⊥MN于OO′,
∵BB′⊥MN.OO′⊥MN,CC′⊥MN,DD′⊥MN,AA′⊥MN,
∴BB′∥OO′∥CC′∥DD′∥AA′,
∴B′O′=O′D′,A′O′=O′C′,
∴AA′+CC′=2OO′,BB′+DD′=2OO′,
∴AA′+CC′=BB′+DD′,
故答案为AA′+CC′=BB′+DD′
(ⅱ)当A点在MN的一侧,点B、C、D在另一侧,如图3中,
如图3中,连接AC、BD交于点O,作OO′⊥MN于OO′,延长A′O交CC′于E.
∵BB′⊥MN.OO′⊥MN,CC′⊥MN,DD′⊥MN,AA′⊥MN,
∴BB′∥OO′∥CC′∥DD′∥AA′,
∴B′O′=O′D′,A′O′=O′C′,
∴BB′+DD′=2OO′,
∵AA′∥CE,
∴∠AA′O=∠OEC
 ,
,
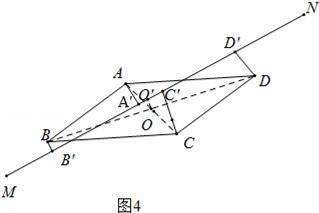
在△AA′O和△CEO中,
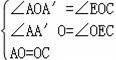
 ,
,
∴△AA′O≌△CEO,
∴AA′=EC,A′O=OE,
∴EC′=2OO′,即CC′﹣AA′=2OO′,
∴CC′﹣AA′=BB′+DD′,
故答案为CC′﹣AA′=BB′+DD.
(ⅲ)当点A、B在MN的一侧,点C、D在另一侧,
如图4中,连接AC、BD交于点O,作OO′⊥MN于OO′,
∵BB′⊥MN.OO′⊥MN,CC′⊥MN,DD′⊥MN,AA′⊥MN,
∴BB′∥OO′∥CC′∥DD′∥AA′,
∴B′O′=O′D′,A′O′=O′C′,
同理可以证明:CC′﹣AA′=2OO′,DD′﹣BB′=2OO′,
∴CC′﹣AA′=DD′﹣BB′,
故答案为CC′﹣AA′=DD′﹣BB′.




【点评】本题考查平行四边形的性质、三角形的中位线定理、梯形的中位线定理、全等三角形的判定和性质,解题的关键是正确添加辅助线,利用中位线定理解决问题,题目有点难度,学会转化的思想,把问题转化为三角形中位线、梯形中位线解决.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
如图,OP=1,过P作PP1⊥OP且PP1=1,得OP1= ;再过P1作P1P2⊥OP1且P1P2=1,得OP2=
;再过P1作P1P2⊥OP1且P1P2=1,得OP2= ;又过P2作P2P3⊥OP2且P2P3=1,得OP3=2…依此法继续作下去,得
;又过P2作P2P3⊥OP2且P2P3=1,得OP3=2…依此法继续作下去,得 = .
= .

查看答案和解析>>
科目:初中数学 来源: 题型:
为了解某校学生每日运动量,收集数据正确的是( )
A.调查该校七年级学生每日运动量;
B.调查该校女生每日的运动量
C.调查该校男生每日的运动量;
D.从七、八、九年级各抽调100人调查他们每日的运动量
查看答案和解析>>
科目:初中数学 来源: 题型:
下列各组长度的线段能组成直角三角形的是( )
A.a=2,b=3,c=4 B.a=4,b=4,c=5
C.a=5,b=6,c=7 D.a=5,b=12,c=13
查看答案和解析>>
科目:初中数学 来源: 题型:
某养鱼专业户年初在鱼塘中投放了500条草鱼苗,6个月后从中随机捞取17条草鱼,称重如下:
| 草鱼质量(单位:千克) | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 | 1.85 | 1.90 |
| 草鱼数量(单位:条) | 2 | 3 | 2 | 3 | 4 | 1 | 1 |
|
 估计这鱼塘中年初投放的500条草鱼此时的总质量大约为多少千克( )
估计这鱼塘中年初投放的500条草鱼此时的总质量大约为多少千克( )
A.845 B.854 C.846 D.847
查看答案和解析>>
科目:初中数学 来源: 题型:
为了解本科生的就业状况,今年3月,某网站对本科生的签约状况进行了网络调查.截止3月底,参与网络调查的12000人中,只有4320人已与用人单位签约.在这个网络调查中,样本容量是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
为了研究某的高度h(千米)与温度t(℃)之间的关系,某日研究人员在该地的不同高度处同时进行了若干次实验,测得的数据如下表:
| h/千米 | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | … |
| t/℃ | 23 | 21 | 19 | 17 | 15 | 13 | 11 | … |
(1)在直角坐标系中,作出各组有序数对(h,t)所对应的点.
(2)这些点是否近似在一条直线上?
(3)估计此时3.5千米高度处的温度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com