
 如图,直角三角形ABC中,∠C=90°,P,E分别是边AB,BC上的点,D为△ABC外一点,DE⊥BC,DE=EC,BE=2EC,∠BDE=∠PEC,AD∥PE,AC=4,则线段BC的长为
如图,直角三角形ABC中,∠C=90°,P,E分别是边AB,BC上的点,D为△ABC外一点,DE⊥BC,DE=EC,BE=2EC,∠BDE=∠PEC,AD∥PE,AC=4,则线段BC的长为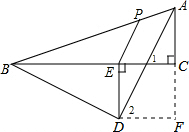 作DF⊥AC,交AC的延长线于F点,如图,
作DF⊥AC,交AC的延长线于F点,如图,
|


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com