
����Ŀ����������������������ߣ���ˮ���Ѿ�������������ͨ���ռ�ͥ��ij������˾����ÿ̨���۷ֱ�Ϊ2000Ԫ��1700Ԫ��A��B�����ͺŵľ�ˮ�����±��ǽ����ܵ����������
����ʱ�� | �������� | �������� | |
A���ͺ� | B���ͺ� | ||
��һ�� | 3̨ | 5̨ | 18000Ԫ |
�ڶ��� | 4̨ | 10̨ | 31000Ԫ |
��1����A��B�����ͺŵľ�ˮ�������۵��ۣ�
��2����������˾���ò�����54000Ԫ�Ľ���ڲɹ��������ͺŵľ�ˮ����30̨����A���ͺŵľ�ˮ������ܲɹ�����̨��
��3���ڣ�2���������£���˾��������30̨��ˮ���ܷ�ʵ������Ϊ12800Ԫ��Ŀ�ꣿ���ܣ��������Ӧ�IJɹ������������ܣ���˵�����ɣ�
���𰸡�
��1���⣺��A��B���־�ˮ�������۵��۷ֱ�ΪxԪ��yԪ��
������ã� ![]() ��
��
��ã� ![]() ��
��
��A��B���־�ˮ�������۵��۷ֱ�Ϊ2500Ԫ��2100Ԫ��
��2���⣺��ɹ�A���ͺž�ˮ��ą����ɹ�B�־�ˮ����30��a��̨��
������ã�2000a+1700��30��a����54000��
��ã�a��10��
�ʳ������ɹ�A���ͺž�ˮ��10̨ʱ���ɹ�������54000Ԫ
��3���⣺������ã���2500��2000��a+��2100��1700����30��a��=12800��
��ã�a=8��
�ʲɹ�A���ͺž�ˮ��8̨���ɹ�B���ͺž�ˮ��22̨����˾��ʵ������12800Ԫ��Ŀ��
����������1����A��B�����ͺž�ˮ�������۵��۷ֱ�ΪxԪ��yԪ������3̨A�ͺ�5̨B�ͺŵľ�ˮ������18000Ԫ��4̨A�ͺ�10̨B�ͺŵľ�ˮ������31000Ԫ���з�������⣻��2����ɹ�A���ͺž�ˮ��ą����ɹ�B���ͺž�ˮ����30��a��̨�����ݽ�����54000Ԫ���в���ʽ��⣻��3��������Ϊ12800Ԫ���з������a��ֵΪ8�����ϣ�2������������֪��ʵ��Ŀ�꣮


 �Ǽ�����������ϵ�д�
�Ǽ�����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
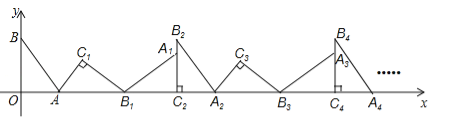
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����ABO�Ƶ�A˳ʱ����ת����AB1C1��λ�ã���B��O�ֱ����ڵ�B1��C1������B1��x���ϣ��ٽ���AB1C1�Ƶ�B1˳ʱ����ת����A1B1C2��λ�ã���C2��x���ϣ�����A1B1C2�Ƶ�C2˳ʱ����ת����A2B2C2��λ�ã���A2��x���ϣ����ν�����ȥ��������A��![]() ��0����B��0��2�������B2016������Ϊ ��
��0����B��0��2�������B2016������Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ľ�����ڶ����ĵ�ļ�����(����)
A.Բ���ⲿB.Բ���ڲ�C.ԲD.Բ���ڲ���Բ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������ε����ߵij��ֱ���5cm��7cm���������ܳ�Ϊ____________cm.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һԪ���η���x2��4x��5��0�������ֱ���x1��x2����ô (1+x1)(1+x2)��ֵ��__��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������һ����Ȼ������λ�ϵ����ִ����λ����λ�����ų���һ�����֣���Ӹ�λ�����λ�����ų���һ��������ȫ��ͬ����ô���ǰ���������Ȼ����Ϊ����г������������Ȼ��12321�������λ����λ�����ų���һ�������ǣ�1��2��3��2��1���Ӹ�λ�����λ�����ų���һ���������ǣ�1��2��3��2��1�����12321��һ������г�������ټ�22��545��3883��345543���������ǡ���г������
��1������ֱ��д��3����λ����г�����������������һ����λ����г�����ܷ�11��������˵�����ɣ�
��2����֪һ���ܱ�11��������λ����г�����������λ�ϵ�����x��1��x��4��xΪ��Ȼ������ʮλ�ϵ�����Ϊy����y��x�ĺ�����ϵʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ȱߡ�ABC�߳�Ϊ6��AD�ǡ�ABC�����ߣ�PΪ�߶�AD���������˵�A��D����һ���㣬��CPΪһ������CP���·�����ͼ��ʾ�ĵȱߡ�CPE������BE��
��1����P���˶������У��߶�BE��APʼ�������˵˵������ɣ�
��2�����ӳ�BE��F��ʹ��CF=CE=5����ͼ2���ʣ������ʱAP�ij���
��3������P���߶�AD���ӳ�����ʱ��FΪ�߶�BE��һ�㣬ʹ��CF=CE=5����EF�ij�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com