
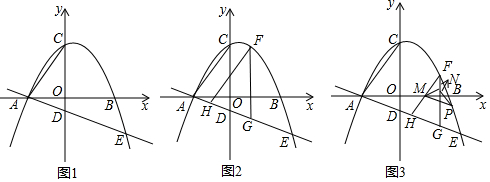
分析 (1)求出A、E两点坐标,利用待定系数法即可解决问题.
(2)如图1中,设F(m,-$\frac{1}{3}$m2+$\frac{1}{3}$m+4),则G(m,-$\frac{1}{3}$m-1),FG=-$\frac{1}{3}$m2+$\frac{2}{3}$m+5,首先判断当FG最大时,△FGH的周长最短,利用二次函数的性质,求出点F坐标,作点F关于y轴的对称点F′,连接AF′,由此AF′交y轴于T,此时|TA-TF|最大,求出直线AF′的解析式即可解决问题.
(3)①如图2中,当∠MNP=90°,重叠部分是△MNP是直角三角形,②如图3中,当PM⊥GF时,重叠部分是△MNK是直角三角形.分别列出方程求解即可.
解答 解:(1)对于抛物线y=-$\frac{1}{3}$x2+$\frac{1}{3}$x+4,令y=0得-$\frac{1}{3}$x2+$\frac{1}{3}$x+4=0,解得x=-3或4.
令x=0得y=4,
∴A(-3,0),B(4,0),C(0,4),
∵x=5时,y=-$\frac{8}{3}$,
∴E(5,-$\frac{8}{3}$),
设直线AD的解析式为y=kx+b,则有$\left\{\begin{array}{l}{-3k+b=0}\\{5k+b=-\frac{8}{3}}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{1}{3}}\\{b=-1}\end{array}\right.$,
∴直线AD的解析式为y=-$\frac{1}{3}$x-1.
(2)如图1中,设F(m,-$\frac{1}{3}$m2+$\frac{1}{3}$m+4),则G(m,-$\frac{1}{3}$m-1),FG=-$\frac{1}{3}$m2+$\frac{2}{3}$m+5,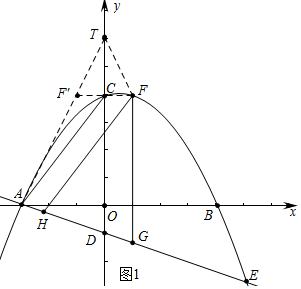
∵FG∥CD,FH∥AC,
∴∠FHC=∠CAD,∠FGH=∠CDA,
∴∠FGH,∠FHG是定值,
∴当FG最大时,△FGH的周长最短,
∵FG=-$\frac{1}{3}$m2+$\frac{2}{3}$m+5=-$\frac{1}{3}$(m-1)2+$\frac{16}{3}$,
∵-$\frac{1}{3}$<0,
∴m=1时,FG有最大值,此时F(1,4),
作点F关于y轴的对称点F′,连接AF′,由此AF′交y轴于T,此时|TA-TF|最大,
∵A(-3,0),F′(-1,4),
∴直线AF′的解析式为y=2x+6,
∴点T坐标(0,6).
(3)①如图2中,当∠MNP=90°,重叠部分是△MNP是直角三角形,
∵△FMN∽△COA,
∴$\frac{FN}{CO}$=$\frac{FM}{AC}$,∵FN=-$\frac{1}{3}$m2+$\frac{1}{3}$m+4,
∴FM=PM=PG=$\frac{5}{4}$FN=$\frac{5}{4}$(-$\frac{1}{3}$m2+$\frac{1}{3}$m+4),
∵2FN+PG=FG,
∴2(-$\frac{1}{3}$m2+$\frac{1}{3}$m+4)+$\frac{5}{4}$(-$\frac{1}{3}$m2+$\frac{1}{3}$m+4)═-$\frac{1}{3}$m2+$\frac{2}{3}$m+5,
整理得9m2-5m-96=0,
解得m=$\frac{32}{9}$或-3(舍弃),
∴FN=-$\frac{1}{3}$($\frac{32}{9}$)2+$\frac{1}{3}$×$\frac{32}{9}$+4=$\frac{236}{243}$.
②如图3中,当PM⊥GF时,重叠部分是△MNK是直角三角形.
∵KM:FK:FM=3:4:5,PM=PG,
∴PK:PG=2:5,
∴KG:PK=$\sqrt{21}$:2,
∴($\frac{1}{3}$m+1):$\frac{1}{2}$(-$\frac{1}{3}$m2+$\frac{1}{3}$m+3)=$\sqrt{21}$:4,
∴(m+3):(m+3)(-m+4)=$\sqrt{21}$:4,
解得m=4-$\frac{4\sqrt{21}}{21}$或-3(舍弃),
∴FK=$\frac{28\sqrt{63}}{63}$-$\frac{16}{63}$.
∵FN:NK=FM:MK=5:3,
∴FN=$\frac{5}{8}$FK=$\frac{35\sqrt{21}}{126}$-$\frac{10}{63}$.
③当∠NMF=90°,不可能得到PM=PG,故此种情形不存在.
综上所述,当△PMN与△FGH重叠部分图形为直角三角形,且PM=PG时,线段FN的长为$\frac{236}{243}$或$\frac{35\sqrt{21}}{126}$-$\frac{10}{63}$.
点评 本题考查二次函数综合题、最值问题、一次函数的应用、勾股定理、直角三角形的判定和性质等知识,解题的关键是学会构建二次函数,利用二次函数的性质解决最值问题,学会用方程的思想思考问题,题目比较难,属于中考压轴题.


科目:初中数学 来源: 题型:选择题
| A. | ∠A=∠D,∠C=∠F,AC=EF | |
| B. | AB=DE,BC=EF,∠A=∠D | |
| C. | ∠A=∠D,∠B=∠E,∠C=∠F | |
| D. | AB=DE,AC=DF,BC边上的高等于EF边上的高 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,一根起点为0的数轴,现有同学将它弯折,弯折后虚线上第一行的数是0,第二行的数是6,第三行的数是21,…,第六行的数是( )
如图,一根起点为0的数轴,现有同学将它弯折,弯折后虚线上第一行的数是0,第二行的数是6,第三行的数是21,…,第六行的数是( )| A. | 78 | B. | 120 | C. | 145 | D. | 171 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点E,F是正方形ABCD的对角线BD所在直线上的两点,且BE=DF,∠EAB=15°.则$\frac{BE}{AB}$=$\frac{\sqrt{6}-\sqrt{2}}{2}$.
如图,点E,F是正方形ABCD的对角线BD所在直线上的两点,且BE=DF,∠EAB=15°.则$\frac{BE}{AB}$=$\frac{\sqrt{6}-\sqrt{2}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
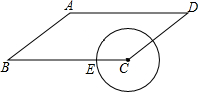 如图,已知平行四边形ABCD中,AB=5,BC=8,cosB=$\frac{4}{5}$,点E是BC边上的动点,当以CE为半径的⊙C与边AD不相交时,半径CE的取值范围是( )
如图,已知平行四边形ABCD中,AB=5,BC=8,cosB=$\frac{4}{5}$,点E是BC边上的动点,当以CE为半径的⊙C与边AD不相交时,半径CE的取值范围是( )| A. | 0<CE≤8 | B. | 0<CE≤5 | C. | 0<CE<3或5<CE≤8 | D. | 3<CE≤5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com