
已知某工厂计划用库存的302m3木料为某学校生产500套桌椅,供该校1250名学生使用,该厂生产的桌椅分为A,B两种型号,有关数据如下:
| 桌椅型号 | 一套桌椅所坐学生人数(单位:人) | 生产一套桌椅所需木材(单位:m3) | 一套桌椅的生产成本(单位:元) | 一套桌椅的运费(单位:元) |
| A | 2 | 0.5 | 100 | 2 |
| B | 3 | 0.7 | 120 | 4 |
(1)y=﹣22x+62000,(240≤x≤250);
(2)生产甲型桌椅250套,乙型桌椅250套,最少总费用56500元.
解析试题分析:(1)利用总费用y=生产桌椅的费用+运费列出函数关系,根据需用的木料不大于302列出一个不等式,两种桌椅的椅子数不小于学生数1250列出一个不等式,两个不等式组成不等式组,得出x的取值范围;
(2)利用一次函数的增减性即可确定费用最少的方案以及费用.
试题解析:(1)设生产甲型桌椅x套,则生产乙型桌椅的套数(500﹣x)套,
根据题意得, ,
,
解这个不等式组得,240≤x≤250;
总费用y=(100+2)x+(120+4)(500﹣x)=102x+62000﹣124x=﹣22x+62000,
即y=﹣22x+62000,(240≤x≤250);
(2)∵y=﹣22x+62000,﹣22<0,
∴y随x的增大而减小,
∴当x=250时,总费用y取得最小值,
此时,生产甲型桌椅250套,乙型桌椅250套,最少总费用y=﹣22×250+62000=56500元.
考点:1、一元一次不等式组的应用;2、一次函数的应用


科目:初中数学 来源: 题型:解答题
直线y= 和x轴,y轴分别交于点E,F,点A是线段EF上一动点(不与点E重合),过点A作x轴垂线,垂足是点B,以AB为边向右作矩形ABCD,AB:BC=3:4。
和x轴,y轴分别交于点E,F,点A是线段EF上一动点(不与点E重合),过点A作x轴垂线,垂足是点B,以AB为边向右作矩形ABCD,AB:BC=3:4。
(1)当点A与点F重合时,求证:四边形ADBE是平行四边形,并求直线DE的表达式;
(2)当点A不与点F重合时,四边形ADBE仍然是平行四边形?说明理由,此时你还能求出直线DE的表达式吗?若能,请你求出来。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
小明家距离学校8千米,今天早晨小明骑车上学途中,自行车突然“爆胎”,恰好路边有便民服务点,几分钟后车修好了,他加快速度骑车到校,我们根据小明的这段经历画了一幅图象,该图描绘了小明行驶路程s与所用时间t之间的函数关系,请根据图象回答下列问题:
(1)小明骑车行驶了多少千米时,自行车“爆胎”修车用了几分钟?
(2)小明共用多长时间到学校的?
(3)小明修车前的速度和修车后的速度分别是多少?
(4)如果自行车未“爆胎”,小明一直按修车前速度行驶,那么他比实际情况早到或晚到多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐标为(2,3).双曲线y= (x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
(x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
(1)求k的值及点E的坐标;
(2)若点F是OC边上一点,且△FBC∽△DEB,求直线FB的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
在一次蜡烛燃烧实验中,蜡烛燃烧时剩余部分的高度y(cm)与燃烧时间x(h)之间为一次函数关系.根据图象提供的信息,解答下列问题:
(1)求出蜡烛燃烧时y与x之间的函数关系式;
(2)求蜡烛从点燃到燃尽所用的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,点A(1,6)和点M(m,n)都在反比例函数y= (x>0)的图象上,
(x>0)的图象上,
(1)k的值为 ;
(2)当m=3,求直线AM的解析式;
(3)当m>1时,过点M作MP⊥x轴,垂足为P,过点A作AB⊥y轴,垂足为B,试判断直线BP与直线AM的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知:直线y=x+1经过点B(2,n),且与x轴交于点A.
(1)求n及点A坐标.
(2) 若点P是x轴上一点,且△APB的面积为6,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知一次函数y=x+b的图象与x轴,y轴交于点A、B.
(1)若将此函数图象沿x轴向右平移2个单位后经过原点,则b= ;
(2)若函数y1=x+b图象与一次函数y2=kx+4的图象关于y轴对称,求k、b的值;
(3)当b>0时,函数y1=x+b图象绕点B逆时针旋转n°(0°<n°<180°)后,对应的函数关系式为y=- x+b,求n的值.
x+b,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:计算题
已知直线 与
与 轴交于点A(-4,0),与
轴交于点A(-4,0),与 轴交于点B.
轴交于点B.
【小题1】求b的值
【小题2】把△AOB绕原点O顺时针旋转90°后,点A落在 轴的
轴的 处,点B若在
处,点B若在 轴的
轴的 处;
处;
①求直线 的函数关系式;
的函数关系式;
②设直线AB与直线 交于点C,矩形PQMN是△
交于点C,矩形PQMN是△ 的内接矩形,其中点P,Q在线段
的内接矩形,其中点P,Q在线段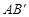 上,点M在线段
上,点M在线段 上,点N在线段AC上.若矩形PQMN的两条邻边的比为1∶2,试求矩形PQMN的周长.
上,点N在线段AC上.若矩形PQMN的两条邻边的比为1∶2,试求矩形PQMN的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com