
如图,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐标为(2,3).双曲线y= (x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
(x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
(1)求k的值及点E的坐标;
(2)若点F是OC边上一点,且△FBC∽△DEB,求直线FB的解析式.
(1)k=3, 点纵坐标为(2,
点纵坐标为(2,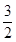 );(2)
);(2) .
.
解析试题分析:(1)根据题意易知D(1,3),把D(1,3)代入y= ,从而求出k=3;然后把E点的横坐标代入y=
,从而求出k=3;然后把E点的横坐标代入y=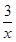 ,求出y的值,从而确定E点坐标;
,求出y的值,从而确定E点坐标;
(2)由(1)易求出BD、BE、BC的值,因为△FBC∽△DEB,根据相似三角形的性质,可求出DF的值,从而确定F点的坐标,根据待定系数法可求出FB的直线解析式.
试题解析:(1)在矩形OABC中, ∵B点坐标为(2,3),
∴BC边中点D的坐标为(1,3)
又∵双曲线y= 的图像经过点D(1,3)
的图像经过点D(1,3)
∴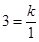 ,
,
∴k=3
∵E点在AB上,
∴E点的横坐标为2.
又∵y=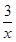 ,经过点E,
,经过点E,
∴E点纵坐标为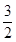 ,
,
∴E点纵坐标为(2,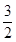 )
)
(2)由(1)得,BD=1,BE=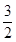 ,BC=2,
,BC=2,
∵△FBC∽△DEB,
∴ ,即
,即 .
.
∴ ,
,
∴ ,即点F的坐标为
,即点F的坐标为
设直线FB的解析式为 ,而直线FB经过B(2,3),F(0,
,而直线FB经过B(2,3),F(0,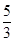 )
)
∴ ,解得
,解得
∴直线FB的解析式为
考点: 一次函数与反比例函数的综合题.


科目:初中数学 来源: 题型:解答题
画出函数y=﹣x+1的图象,结合图象,回答下列问题.
在函数y=﹣x+1的图象中:
(1)画出函数图象并写出与x轴的交点坐标是 _________ ;
(2)随着x的增大,y将 _________ (填“增大”或“减小”);
(3)当y取何值时,x<0? _________
(4)把它的图象向下平移2个单位长度则得到的新的一次函数解析式是 _________ .
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
张先生准备在沙坪坝购买一套小户型商品房,他去某楼盘了解情况得知, 该户型商品房的单价是8000元/ ,面积如图所示(单位:米,卫生间的宽未定,设宽为
,面积如图所示(单位:米,卫生间的宽未定,设宽为 米),售房部为张先生提供了以下两种优惠方案:
米),售房部为张先生提供了以下两种优惠方案:
方案一:整套房的单价是8000元/ ,其中厨房可免费赠送
,其中厨房可免费赠送 的面积;
的面积;
方案二:整套房按原销售总金额的9折出售.
(1)用 表示方案一中购买一套该户型商品房的总金额,用
表示方案一中购买一套该户型商品房的总金额,用 表示方案二中购买一套该户型商品房的总金额,分别求出
表示方案二中购买一套该户型商品房的总金额,分别求出 、
、 与
与 的关系式;
的关系式;
(2)求 取何值时,两种优惠方案的总金额一样多?
取何值时,两种优惠方案的总金额一样多?
(3)张先生因现金不够,于2012年1月在建行借了9万元住房贷款,贷款期限为6年,从开始贷款的下一个月起逐月偿还,贷款月利率是0.5%,每月还款数额=平均每月应还的贷款本金数额+月利息,月利息=上月所剩贷款本金数额×月利率.
①张先生借款后第一个月应还款数额是多少元?
②假设贷款月利率不变,若张先生在借款后第 (
( ,
, 是正整数)个月的还款数额为P,请写出P与
是正整数)个月的还款数额为P,请写出P与 之间的关系式.
之间的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知一次函数y=kx+b,当x=2时,y=﹣3,当x=1时,y=﹣1.
(1)求一次函数的解析式;
(2)若该一次函数的图形交x轴y轴分别于A、B两点,求△ABO的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知某工厂计划用库存的302m3木料为某学校生产500套桌椅,供该校1250名学生使用,该厂生产的桌椅分为A,B两种型号,有关数据如下:
| 桌椅型号 | 一套桌椅所坐学生人数(单位:人) | 生产一套桌椅所需木材(单位:m3) | 一套桌椅的生产成本(单位:元) | 一套桌椅的运费(单位:元) |
| A | 2 | 0.5 | 100 | 2 |
| B | 3 | 0.7 | 120 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系xOy中,一次函数y=ax+b的图象与x轴相交于点A(-2,0),与y轴交于点C,与反比例函数 在第一象限内的图象交于点B(m,n),连结OB.若S△AOB=6,S△BOC=2.
在第一象限内的图象交于点B(m,n),连结OB.若S△AOB=6,S△BOC=2.
(1)求一次函数的表达式;
(2)求反比例函数的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在平面直角坐标系中,点O坐标原点,直线l分别交x轴、y轴于A,B两点,OA<OB,且OA、OB的长分别是一元二次方程 的两根.
的两根.
(1)求直线AB的函数表达式;
(2)点P是y轴上的点,点Q第一象限内的点.若以A、B、P、Q为顶点的四边形是菱形,请直接写出Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
温州享有“中国笔都”之称,其产品畅销全球,某制笔企业欲将n件产品运往A,B,C三地销售,要求运往C地的件数是运往A地件数的2倍,各地的运费如图所示.设安排x件产品运往A地.
(1)当n=200时,
①根据信息填表:
| | A地 | B地 | C地 | 合计 |
| 产品件数(件) | x | | 2x | 200 |
| 运费(元) | 30x | | | |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
如图,一个装有进水管和出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分)之间的部分关系.那么,从关闭进水管起 分钟该容器内的水恰好放完.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com