
解:
①等腰直角三角形.
连接AO,在△ABC中,∠CAB=90°,AB=AC,O为BC的中点,
∴AO⊥BC,AO=OB,∠NAO=45°,
又∵∠B=45°,AN=BM,
∴△AON≌△BOM,
∴ON=OM,∠AON=∠BOM.
∵∠BOM+∠AOM=90°,
∴∠AON+∠AOM=90°,即∠MON=90°,
所以△MON是等腰直角三角形;
②不变.
∵△AON≌△BOM
∴S
四边形AMON=S
△AOB=
S
△ABC,所以不变;
③y=S
△OMN=S
四边形AMON-S
△AMN=

S
△ABC-

AN•AM
=

-

x(

-x)=2-

x(2

-x)=-

x
2-

x+2(0<x<2

)
∵-

<0,
∴函数有最大值,当x=-

=

时,属于0<x<2

,y最大=

=1.
分析:①先从直观上猜想,再从理论上寻找依据.从O为BC的中点想到直角三角形斜边上的中线等于斜边的一半,所以连OA,利用等腰三角形的性质结合AN=BM,易证△AON≌△BOM,判断△OMN的形状;
②根据△AON≌△BOM,易证四边形AMON的面积=△AOB的面积=

S
△ABC,所以不变;
③S
△OMN=S
四边形AMON-S
△AMN=

S
△ABC-

AN•AM,据此得函数表达式求解.
点评:直角三角形中连接直角顶点和斜边中点构成斜边上的中线是常作的辅助线.

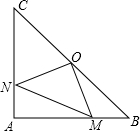 如图:在△ABC中,∠CAB=90°,AB=AC,O为BC的中点,M,N分别在AB,AC上,且AN=BM.
如图:在△ABC中,∠CAB=90°,AB=AC,O为BC的中点,M,N分别在AB,AC上,且AN=BM. ,△OMN的面积为y,求y关于x的关系式,并求当x为何值时,y的值最大.
,△OMN的面积为y,求y关于x的关系式,并求当x为何值时,y的值最大. 解:
解: S△ABC,所以不变;
S△ABC,所以不变; S△ABC-
S△ABC- AN•AM
AN•AM -
- x(
x( -x)=2-
-x)=2- x(2
x(2 -x)=-
-x)=- x2-
x2- x+2(0<x<2
x+2(0<x<2 )
) <0,
<0, =
= 时,属于0<x<2
时,属于0<x<2 ,y最大=
,y最大= =1.
=1. S△ABC,所以不变;
S△ABC,所以不变; S△ABC-
S△ABC- AN•AM,据此得函数表达式求解.
AN•AM,据此得函数表达式求解.

 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为