
分析 由于正方形的位置不确定要分两种情况讨论:①正方形有一个顶点在斜边上,可设出正方形的边长,利用相似三角形的成比例线段求解;②正方形有两个顶点在斜边上;可设出正方形的边长,利用相似三角形的成比例线段求解.
解答 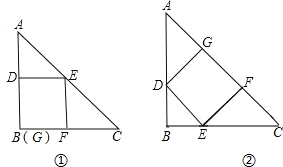 解:如图;
解:如图;
Rt△ABC中,AB=6cm,BC=8cm,由勾股定理,得:
AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=10(cm);
(1)如图①,设正方形的边长为xcm,则AD=3-x,CF=4-x;
易证得△ADE∽△EFC;
∴$\frac{DE}{FC}=\frac{AD}{EF}$,即$\frac{x}{8-x}=\frac{6-x}{x}$,解得x=$\frac{24}{7}$;
即正方形的边长为$\frac{24}{7}$cm;
(2)如图②,设正方形的边长为xcm,则AG=$\frac{3}{4}$x,CF=$\frac{4}{3}$x;
∴AC=AG+EF+CF=$\frac{3}{4}$x+$\frac{4}{3}$x+x=10,解得x=$\frac{120}{37}$;
即正方形的边长为$\frac{120}{37}$cm;
故这个正方形的边长为$\frac{24}{7}$cm或$\frac{120}{37}$cm;
故答案为:$\frac{24}{7}$cm或$\frac{120}{37}$cm.
点评 此题主要考查了正方形的性质、相似三角形的判定和性质、勾股定理的应用等知识,同时还考查了分类讨论的数学思想方法.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
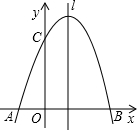 已知,点C在y轴上,OC=3,将线段OC绕点O顺时针旋转90°至OB的位置,点A的横坐标为方程x2-1=0的一个解且点A、B在y轴两侧.
已知,点C在y轴上,OC=3,将线段OC绕点O顺时针旋转90°至OB的位置,点A的横坐标为方程x2-1=0的一个解且点A、B在y轴两侧.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com