【题目】如图，身高1.6米的小明从距路灯的底部（点O）20米的点A沿AO方向行走14米到点C处，小明在A处，头顶B在路灯投影下形成的影子在M处．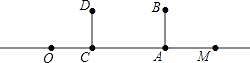
（1）已知灯杆垂直于路面，试标出路灯P的位置和小明在C处，头顶D在路灯投影下形成的影子N的位置．
（2）若路灯（点P）距地面8米，小明从A到C时，身影的长度是变长了还是变短了？变长或变短了多少米？
科目：初中数学 来源： 题型：
【题目】定义：如果一个分式能化成一个整式与一个分子为常数的分式的和的形式，则称这个分式为“和谐分式”．如：
，则
是“和谐分式”．
(1)下列分式中，属于“和谐分式”的是_____(填序号)；
①
；②
；③
；④
；
(2)将“和谐分式”
化成一个整式与一个分子为常数的分式的和的形式为：＝_______(要写出变形过程)；
(3)应用：先化简
，并求x取什么整数时，该式的值为整数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在△ABC和△A′B′C′中，①AB=A′B′，②BC=B′C′，③AC=A′C′，④∠A=∠A′，⑤∠B=∠B′，⑥∠C=∠C′，则下列各组条件中使△ABC和△A′B′C′全等的是（ ）
A. ④⑤⑥ B. ①②⑥ C. ①③⑤ D. ②⑤⑥
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在△ABC中，∠A=150°．第一步：在△ABC上方确定一点A1，使∠A1BA=∠ABC，∠A1CA=∠ACB，如图1.第二步：在△A1BC上方确定一点A2，使∠A2BA1=∠A1BA，∠A2CA1=∠A1CA，如图2．照此下去，至多能进行( )步．
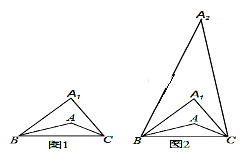
A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知AB是⊙O的直径，弦CD⊥AB于点E，点M在⊙O上，∠M=∠D．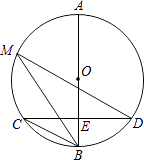 
（1）判断BC、MD的位置关系，并说明理由；
（2）若AE=16，BE=4，求线段CD的长；
（3）若MD恰好经过圆心O，求∠D的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
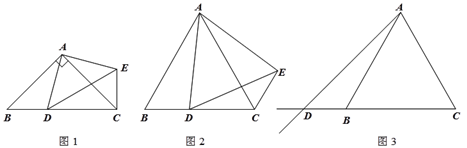
【题目】（1）如图①，在四边形ABCD中，AB∥DC，E是BC的中点，若AE是∠BAD的平分线，求证：AD=DC+AB，
（2）如图②，在四边形ABCD中，AB∥DC，F是DC延长线上一点，连接AF，E是BC的中点，若AE是∠BAF的平分线，求证：AB=AF+CF.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如∠MON＝30°、OP＝6，点A、B分别在OM、ON上；（1）请在图中画出周长最小的△PAB（保留画图痕迹）；（2）请求出（1）中△PAB的周长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在△ABC中，AB=AC，点D是射线CB上的一动点（不与点B、C重合），以AD为一边在AD的右侧作△ADE，使AD=AE，∠DAE=∠BAC，连接CE．
（1）如图1，当点D在线段CB上，且∠BAC=90°时，那么∠DCE= 度；
（2）设∠BAC= 
，∠DCE= 
．
① 如图2，当点D在线段CB上，∠BAC≠90°时，请你探究
与
之间的数量关系，并证明你的结论；
② 如图3，当点D在线段CB的延长线上，∠BAC≠90°时，请将图3补充完整，并直接写出此时
与
之间的数量关系（不需证明）．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
