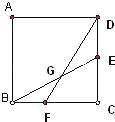
【题目】已知正方形ABCD的边长为4cm，E，F分别为边DC，BC上的点，BF＝1cm，CE＝2cm，BE，DF相交于点G，求四边形CEGF的面积．

参考答案：

【答案】

【解析】试题分析：

如图，以点B为坐标原点，BC所在直线为x轴，建立坐标系，从而可得点A、B、C、D、E、F的坐标并由此求出直线BE和DF的解析式，进而可求得点G的坐标，这样就可计算出△BGF和△BCE的面积，由此即可求得四边形CEGF的面积了.

试题解析：

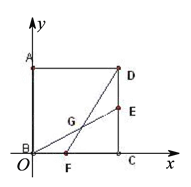
以B点为坐标原点，BC所在直线为x轴建立坐标系，如下图：

由题意可得几个点的坐标A（0，4），B（0，0），C（4，0），D（4，4），E（4，2），F（1，0）．

设BE所在直线的解析式是y＝kx，

∵BE所在直线经过E点，

∴4k＝2，解得：k＝，

∴BE所在直线的解析式是y＝x（1），

同理可得出DF所在直线的解析式是y＝（x－1）（2），

联立（1）、（2）可解得点G的坐标为（，）．

∴四边形CEGF的面积S＝S△BCE－S△BFG＝×4×2－×1×＝．

关闭