练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．李明在计算一个多项式减去x2-2x+1时，误认为加上此式，计算出错误结果为-3x2+2x-1，请求出正确答案．

    分析 根据题意先计算出被减式，然后再进行减法运算即可．

    解答 解：被减式=-3x2+2x-1-（x2-2x+1）
    =-3x2+2x-1-x2+2x-1
    =-4x2+4x-2，
    故可得正确结果=（-4x2+4x-2）-（x2-2x+1）
    =-4x2+4x-2-x2+2x-1
    =-5x2+6x-3．

    点评 此题考查了整式的加减，解决此类题目的关键是熟记去括号法则，熟练运用合并同类项的法则，这是各地中考的常考点．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

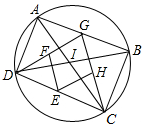    4．如图，AC与BD是⊙I的直径，AD=4，CD=10，点G是AB上一动点，点E、F、H分别是DC、DG、CG的中点．
    （1）求证：四边形EFGH是平行四边形；
    （2）填空：①当AG=5时，四边形EFCH是菱形；
    ②当AG=2或8时，四边形EFGH是矩形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．已知：x≤1，含x的代数式A=3-2x，那么A的值的范围是A≥1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．已知实数m的平方根是5a+1和2a-15，试求a和m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．大于-4而小于+3的整数是-3，-2，-1，0，1，2，绝对值大于2而小于6的所有的整数的和是0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

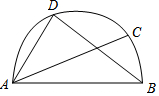    20．如图，AB是半圆的直径，∠BAC=20°，D是$\widehat{AC}$的中点，则∠DAC的度数是（　　）
    A．30°B．35°C．45°D．70°

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．下列说法中正确的是（　　）
    A．2π是有理数B．数轴上表示-a的点一定在原点左边
    C．单项式-$\frac{2}{3}$πa2b的系数为-$\frac{2}{3}$D．多项式x-y的次数是1

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．阅读下面的文字，解答问题：
    大家知道$\sqrt{2}$是无理数，而无理数是无限不循环小数，因此$\sqrt{2}$的小数部分我们不可能全部地写出来，于是小明用$\sqrt{2}$-1来表示$\sqrt{2}$的小数部分，你同意小明的表示方法吗？事实上，小明的表示方法是有道理，因为$\sqrt{2}$的整数部分是1，将这个数减去其整数部分，差就是小数部分．又例如：∵$\sqrt{4}$＜$\sqrt{7}$＜$\sqrt{9}$，即2＜$\sqrt{7}$＜3，∴$\sqrt{7}$的整数部分为2，小数部分为（$\sqrt{7}$-2）．
    请解答：
    （1）如果$\sqrt{5}$的小数部分a=$\sqrt{5}$-2，$\sqrt{13}$的整数部分b=3，则a+b-$\sqrt{5}$=1；
    （2）已知：10+$\sqrt{3}$=x+y，其中整数部分x=11，且0＜y＜1，求x-y的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．甲，乙两只昆虫一开始在数轴上的点A，点B处，它们在数轴上所对应的数分别为-8，4；这两只昆虫各自以一定的速度在数轴上运动，且甲昆虫的运动速度为2个单位/秒．
    （1）若甲、乙两昆虫同时相向而行，在原点处相遇，求乙昆虫的运动速度；
    （2）若甲、乙两昆虫以（1）中的速度同时出发，都沿着数轴的正方向运动，几秒钟时两者相距6个单位长，并求出此时甲昆虫在数轴上所对应的数．

    查看答案和解析>>

    同步练习册答案