
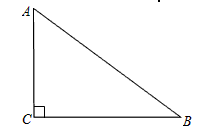
| 解:(1)作图正确, 写出结论:射线AM就是所要求的角平分线; |
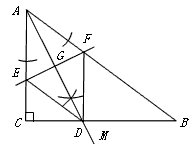 |
| (2)①四边形AEDF是菱形, 证明:如图,根据题意,可知EF是线段AD的垂直平分线, 则AE=ED,AF=FD,∠AGE=∠AGF=90°, 由(1)可知,AD是∠BAC的平分线, ∴∠EAD=∠DAF, ∵∠AGE=∠AGF,AG=AG, ∴△AEG≌△AFG, ∴AE=AF, ∴AE=ED=DF=AF, ∴四边形AEDF是菱形; ②设AE=x,则ED=x,CE=8-x, 在Rt△ECD中,42+(8-x)2=x2, 解得x=5, ∴4x=20, 即四边形AEDF的周长是20, 由①可知,四边形AEDF是菱形, ∴FD∥AC, ∴ 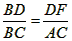 , ,∴ 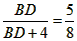 , ,解得 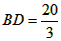 ,即BD的长是 ,即BD的长是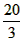 。 。 |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
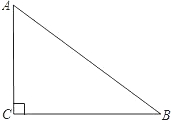 如图所示,已知:Rt△ABC中,∠ACB=90°.
如图所示,已知:Rt△ABC中,∠ACB=90°.查看答案和解析>>
科目:初中数学 来源: 题型:
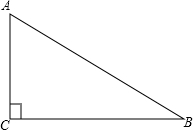 如图所示,已知:Rt△ABC中,∠ACB=90°.
如图所示,已知:Rt△ABC中,∠ACB=90°.查看答案和解析>>
科目:初中数学 来源: 题型:
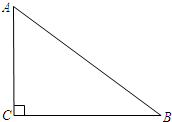 如图所示,已知:Rt△ABC中,∠ACB=90°.
如图所示,已知:Rt△ABC中,∠ACB=90°.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,已知在Rt△ABC中,∠C=90°,BC=4,AC=4,现将△ABC沿射线CB方向平移到△A′B′C′的位置.若平移距离为3,求△ABC与△A′B′C′的重叠部分的面积.
如图所示,已知在Rt△ABC中,∠C=90°,BC=4,AC=4,现将△ABC沿射线CB方向平移到△A′B′C′的位置.若平移距离为3,求△ABC与△A′B′C′的重叠部分的面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com