
 如图所示,已知在Rt△ABC中,∠C=90°,BC=4,AC=4,现将△ABC沿射线CB方向平移到△A′B′C′的位置.若平移距离为3,求△ABC与△A′B′C′的重叠部分的面积.
如图所示,已知在Rt△ABC中,∠C=90°,BC=4,AC=4,现将△ABC沿射线CB方向平移到△A′B′C′的位置.若平移距离为3,求△ABC与△A′B′C′的重叠部分的面积.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源:2013-2014学年广东东莞寮步宏伟中学九年级上学期第三次月考数学试卷(解析版) 题型:填空题
如图所示,已知在Rt△ABC中∠ACB=90°,AB=4,分别以AC,BC为直径作半圆,面积分别记为 ,
, ,则
,则 +
+ 的值等于__________.
的值等于__________.

查看答案和解析>>
科目:初中数学 来源:2012年北师大版初中数学七年级下5.3图案设计练习卷(解析版) 题型:解答题
如图所示,已知在Rt△ABC中,∠ACB=90°,CD是AB边上的高,AB=13 cm,BC=12 cm,AC=5 cm,小明说利用面积关系就能求出CD的长.请你帮他求出CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
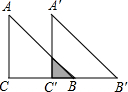 如图所示,已知在Rt△ABC中,∠C=90°,BC=4,AC=4,现将△ABC沿射线CB方向平移到△A′B′C′的位置.若平移距离为3,求△ABC与△A′B′C′的重叠部分的面积.
如图所示,已知在Rt△ABC中,∠C=90°,BC=4,AC=4,现将△ABC沿射线CB方向平移到△A′B′C′的位置.若平移距离为3,求△ABC与△A′B′C′的重叠部分的面积.查看答案和解析>>
科目:初中数学 来源:专项题 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com