
 ��ͼ���ڵ��������ཻ�ڵ�P������PA��x���ڵ�A��PB��y���ڵ�B����֪B��0����6����S��DBP��27.
��ͼ���ڵ��������ཻ�ڵ�P������PA��x���ڵ�A��PB��y���ڵ�B����֪B��0����6����S��DBP��27. ��ͼ�����ABP���й����㣬ֱ��д��n��ȡֵ��Χ.
��ͼ�����ABP���й����㣬ֱ��д��n��ȡֵ��Χ.
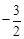 x+3��
x+3��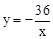 ����2����-4��9����4��-3������3��-36��n��0��
����2����-4��9����4��-3������3��-36��n��0��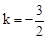 .
.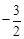 x+3.
x+3. �ã�m=-36.
�ã�m=-36.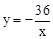 .
.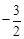 x+3.��ͼ��x���ڵ�C��
x+3.��ͼ��x���ڵ�C��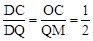 ����MQ=2OC=4.
����MQ=2OC=4.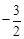 x+3�ã�y=-3������ʱQ�������ǣ�4��-3��.
x+3�ã�y=-3������ʱQ�������ǣ�4��-3��. x+3�ã�y=-3������ʱQ�������ǣ�-4��9��.
x+3�ã�y=-3������ʱQ�������ǣ�-4��9��.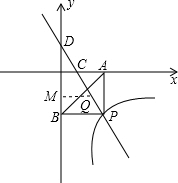
 ��ͼ�����ABP���й����㣬
��ͼ�����ABP���й����㣬


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
 ����
���� ����
���� ����
���� ����
���� �����У���һ�κ������У� ��
�����У���һ�κ������У� ��| A��5 �� | B��4�� | C��3�� | D��2�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
 ,
, ,
, ,������ͼ��ʾ�ķ�ʽ����,��
,������ͼ��ʾ�ķ�ʽ����,�� �͵�
�͵� �ֱ���ֱ��
�ֱ���ֱ�� ��
�� ����,��֪��
����,��֪�� ����
���� �������� .
�������� . 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
 x+8��x�ᣬy��ֱ��ڵ�A��B��M��OB�ϵ�һ�㣬������ABM��AM�۵�����Bǡ������x���ϵĵ�B�䴦����ֱ��AM�Ľ���ʽΪ�� ����
x+8��x�ᣬy��ֱ��ڵ�A��B��M��OB�ϵ�һ�㣬������ABM��AM�۵�����Bǡ������x���ϵĵ�B�䴦����ֱ��AM�Ľ���ʽΪ�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
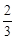 x��b�뷴��������y=
x��b�뷴��������y= �У�x��y�Ķ�Ӧֵ���±���
�У�x��y�Ķ�Ӧֵ���±���
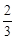 x��b>
x��b> �Ľ⼯Ϊ ��
�Ľ⼯Ϊ ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
 ��������ĺ���ֵΪ��������.
��������ĺ���ֵΪ��������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com