
����Ŀ��������ij��ҵ������Ӧ���������·�չ���ĺ��٣��з���һ���²�Ʒ����֪�з����������ֲ�Ʒ�ijɱ�Ϊ30Ԫ����������������y������������ۼ�x��Ԫ�������ĺ�������ʽΪ��
![]()
��1������ҵ���۸ò�Ʒ����������ΪW����Ԫ������ֱ��д��������W����Ԫ�������ۼ���Ԫ/�����ĺ�������ʽ��
��2�����ò�Ʒ���ۼ�x��Ԫ/����Ϊ����ʱ����ҵ���۸ò�Ʒ��õ����������?����������Ƕ���?
��3������ҵ���۸ò�Ʒ��������������750��Ԫ����ȷ���ò�Ʒ���ۼ�x��Ԫ/������ȡֵ��Χ��
���𰸡���1��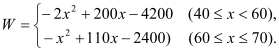 ��2�����ò�Ʒ���ۼ۶�Ϊ50Ԫ����ʱ�����۸ò�Ʒ������������������Ϊ800��Ԫ����3��Ҫʹ��ҵ���۸ò�Ʒ������������750��Ԫ���ò�Ʒ�����ۼ�x��Ԫ/������ȡֵ��ΧΪ45��x��55.
��2�����ò�Ʒ���ۼ۶�Ϊ50Ԫ����ʱ�����۸ò�Ʒ������������������Ϊ800��Ԫ����3��Ҫʹ��ҵ���۸ò�Ʒ������������750��Ԫ���ò�Ʒ�����ۼ�x��Ԫ/������ȡֵ��ΧΪ45��x��55.
��������
�����������1��������������=����������ÿ����Ʒ������ÿ����Ʒ���ۼ�-ÿ����Ʒ�Ľ��ۣ���ֱ���г�ʽ�ӣ����ɣ���2�����ݶ��κ��������ʣ��ֱ�����������������ֵ���Ƚϼ��ɵý��ۣ���3�����ɣ�2���Ľ��ۣ��ų��ڶ���������ٸ��ݶ��κ��������ʣ��ɵ�һ�����ȷ��x��ȡֵ��Χ.
�����������1��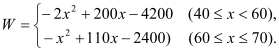
��2������1��֪����540��x<60ʱ��W=-2��x-50��2+800��
��-2<0��������x=50ʱ��W�����ֵ800��
��60��x��70ʱ��W=-��x-55��2+625.
��-1��0�� ����60��x��70ʱ��W��x���������С��
����x=60ʱ��W�����ֵ600��
![]()
�����ò�Ʒ���ۼ۶�Ϊ50Ԫ����ʱ�����۸ò�Ʒ������������������Ϊ800��Ԫ��
��3����40��x��60ʱ����W=750����
-2��x-50��2+800=750,��֮����![]()
�ɺ���W=-2��x-50��2+800�����ʿ�֪��
��45��x��55ʱ��W��750��
��60��x��70ʱ��W���ֵΪ600��750.
���ԣ�Ҫʹ��ҵ���۸ò�Ʒ������������750��Ԫ���ò�Ʒ�����ۼ�x��Ԫ/������ȡֵ��ΧΪ45��x��55.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijһ�ͺŷɻ���½���еľ���y����λ��m���뻬��ʱ��x����λ��s��֮��ĺ�������ʽ��y = 60x��1��5x2�����ͺŷɻ���½���軬�� m����ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ��l��ֱ��y��2x��3����y��Գƣ���ֱ��l�Ľ���ʽ�ǣ�������
A. y����2x+3B. y����2x��3C. y��2x+3D. y��2x��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺��ͼ��1�������ֱ�����ABC������AC��BC��ABΪ���������������������ACDE��BCFG��ABMN�����������������Ϊ��ABC����չ��Ҷ�����Σ�������������������Ϊ��ABC����չ
˫Ҷ�����Σ�
��1������ABC����չ˫Ҷ������ACDE��BCFG������ABC����DCF������ֱ�ΪS1��S2��
����ͼ��2��������ACB=90��ʱ����֤��S1=S2��
����ͼ��3��������ACB��90��ʱ��S1��S2�Ƿ���Ȼ��ȣ���˵�����ɣ�
��2����֪��ABC�У�AC=3��BC=4��������չ��Ҷ�����Σ�����DCF����AEN����BGM�������ΪS��������ͼ��1��̽��������ACB�Ķ��������仯ʱ��S��ֵ�Ƿ����仯�������䣬���S��ֵ�����仯�����S�����ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һԪ���η���x2��x��1��0�ĸ������Ϊ( )
A. ��������ȵ�ʵ����
B. û��ʵ����
C. ����������ȵ�ʵ����
D. ����������ȵ�ʵ����������ʵ������Ϊ1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��O1���O2��Բ�ľ�O1O2��6cm������Բ�İ뾶����һԪ���η���x2-6x+8=0������Բ��λ�ù�ϵΪ��( )
A. ���� B. ���� C. ���� D. �ཻ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij¥��2013�귿��Ϊÿƽ����8100Ԫ�����������������ۺ�2015�귿��Ϊ7600Ԫ�����¥�������귿��ƽ��������Ϊx������������з���Ϊ__________��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com