
如图,在平面直角坐标系xO y中,矩形ABCD的AB边在x轴上,且AB=3,AD=2,经过点C的直线y=x-2与x轴、y轴分别交于点E、F.
y中,矩形ABCD的AB边在x轴上,且AB=3,AD=2,经过点C的直线y=x-2与x轴、y轴分别交于点E、F.
 (1)求矩形ABCD的顶点A、B、C、D的坐标;
(1)求矩形ABCD的顶点A、B、C、D的坐标;
(2)求证:△OEF≌△BEC;
(3)P为直线y=x-2上一点,若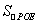 =5,求点P的坐标.
=5,求点P的坐标.
科目:初中数学 来源: 题型:
数学课上,探讨角平分线的作法时,徐老师用直尺和圆规作角平分线,方法如下:
 作法:①如图①,在射线OA、OB上,分别截取OD、OE,使OD=OE;
作法:①如图①,在射线OA、OB上,分别截取OD、OE,使OD=OE;
②分别以点D和点E为圆心,适当长(大于线段DE长的一半)为半径作圆弧,在∠AOB的内部,两弧交于点C;
③作射线OC.
徐老师又介绍用角尺平分一个任意角的方法,作法如下:
如图②,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与点M,N重合,过角尺顶点C的射线OC便是∠AOB的平分线.
(1)徐老师用尺规作图作角平分线时,用到的三角形全等的判定方法是__________;
(2)请证明徐老师用角尺平分一个任意角的 方法.
方法.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在△ABO中,AB⊥OB,OB=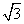 ,AB=1.将△ABO绕O点旋转90°后得到
,AB=1.将△ABO绕O点旋转90°后得到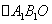 ,则点
,则点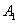 的坐标为……………………………………………( )
的坐标为……………………………………………( )
A.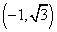 ;B.
;B.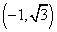 或
或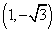 ;C.
;C.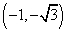 ;D.
;D.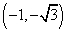 )或
)或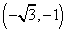 ;
;
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
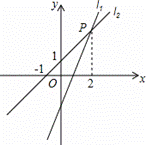 过点(0,-2)的直线
过点(0,-2)的直线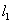 :
: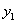 =kx+b(k≠0)与直线
=kx+b(k≠0)与直线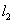 :
: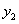 =x+1交于点P(2,m).
=x+1交于点P(2,m).
(1)写出使得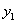 <
<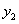 的x的取值范围;
的x的取值范围;
(2)求点P的坐标和直线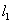 的解析式.
的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com