
△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长为( )
A.42 B.32 C.42或32 D.37或33
C【考点】勾股定理.
【专题】分类讨论.
【分析】本题应分两种情况进行讨论:
①当△ABC为锐角三角形时,在Rt△ABD和Rt△ACD中,运用勾股定理可将BD和CD的长求出,两者相加即为BC的长,从而可将△ABC的周长求出;
②当△ABC为钝角三角形时,在Rt△ABD和Rt△ACD中,运用勾股定理可将BD和CD的长求出,两者相减即为BC的长,从而可将△ABC的周长求出.
【解答】解:此题应分两种情况说明:
①当△ABC为锐角三角形时,在Rt△ABD中,
BD=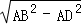 =
= =9,
=9,
在Rt△ACD中,
CD=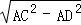 =
=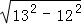 =5
=5
∴BC=5+9=14
∴△ABC的周长为:15+13+14=42;
②当△ABC为钝角三角形时,
在Rt△ABD中,BD=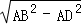 =
=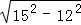 =9,
=9,
在Rt△ACD中,CD= =
= =5,
=5,
∴BC=9﹣5=4.
∴△ABC的周长为:15+13+4=32
综上所述,△ABC的周长为:42或32.
故选C.

【点评】此题考查了勾股定理及解直角三角形的知识,在解本题时应分两种情况进行讨论,易错点在于漏解,同学们思考问题一定要全面,有一定难度.


科目:初中数学 来源: 题型:
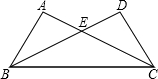
如图,在△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.
(1)求证:△ABE≌△DCE;
(2)当∠AEB=70°时,求∠EBC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平面直角坐标系xO y中,矩形ABCD的AB边在x轴上,且AB=3,AD=2,经过点C的直线y=x-2与x轴、y轴分别交于点E、F.
y中,矩形ABCD的AB边在x轴上,且AB=3,AD=2,经过点C的直线y=x-2与x轴、y轴分别交于点E、F.
 (1)求矩形ABCD的顶点A、B、C、D的坐标;
(1)求矩形ABCD的顶点A、B、C、D的坐标;
(2)求证:△OEF≌△BEC;
(3)P为直线y=x-2上一点,若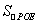 =5,求点P的坐标.
=5,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com