练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

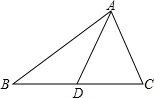
    如图，AD是△ABC的BC边上的中线，若△ABC的面积是6，则△ACD的面积是__________．


    3．

    【考点】三角形的面积．

    【分析】先根据三角形中线的定义可得BC=2BD，然后根据等高的三角形的面积的比等于底边的比求解即可．

    【解答】解：∵AD是△ABC的BC边上的中线，

    ∴BC=2BD，

    ∴S△ABD：S△ABC=BD：BC=1：2．

    ∵△ABC的面积是6，

    ∴△ACD的面积是3．

    故答案为：3．

    【点评】本题考查了三角形的面积，熟记等高的三角形的面积的比等于底边的比是解题的关键．

    1

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图，A，B的坐标为（2，0），（0，1）若将线段AB平移至A1B1，则a+b的值为__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    △ABC中，AB=15，AC=13，高AD=12，则△ABC的周长为(     )

    A．42     B．32     C．42或32   D．37或33

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知，直线m与y的交点在x轴下方，与x轴距离2个单位长度，且直线m过点（1，﹣1）．

    （1）求：直线m的表达式；

    （2）求：直线m与x轴的交点坐标；

    （3）若直线n与直线m在x轴交于同一点，且直线n与直线m以及y轴所围成的三角形面积为4，请直接写出直线n的表达式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    三角形的外角和等于__________度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在△ABF与△CDE中，AB=CD，BF=DE，点A、E、F、C在同一条直线上，AE=CF，求证：△ABF≌△CDE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    数学课上，探讨角平分线的作法时，徐老师用直尺和圆规作角平分线，方法如下：

    作法：①如图①，在射线OA、OB上，分别截取OD、OE，使OD=OE；

    ②分别以点D和点E为圆心，适当长（大于线段DE长的一半）为半径作圆弧，在∠AOB的内部，两弧交于点C；

    ③作射线OC．

    徐老师又介绍用角尺平分一个任意角的方法，作法如下：

    如图②，∠AOB是一个任意角，在边OA，OB上分别取OM=ON，移动角尺，使角尺两边相同的刻度分别与点M，N重合，过角尺顶点C的射线OC便是∠AOB的平分线．

    （1）徐老师用尺规作图作角平分线时，用到的三角形全等的判定方法是__________；

    （2）请证明徐老师用角尺平分一个任意角的方法．

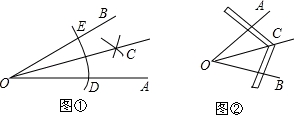
    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知直线与x轴的交点在A（2，0）、B（3，0）之间（包括A、B两点），则的取值范围是              ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


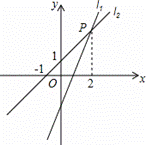    过点（0，-2）的直线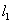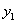：=kx+b（k≠0）与直线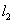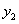：=x+1交于点P（2，m）．

    （1）写出使得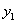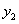＜的x的取值范围； 

    （2）求点P的坐标和直线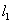的解析式．

    查看答案和解析>>

    同步练习册答案