
如图,在△ABC与△DCB中,AC与BD交于点E,且∠A=∠D,AB=DC.
(1)求证:△ABE≌△DCE;
(2)当∠AEB=70°时,求∠EBC的度数.
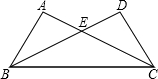
【考点】全等三角形的判定与性质.
【分析】(1)利用“角角边”证明△ABE和△DCE全等即可;
(2)根据全等三角形对应边相等可得BE=CE,再根据邻补角的定义求出∠BEC,然后根据等腰三角形两底角相等列式计算即可得解.
【解答】(1)证明:在△ABE和△DCE中,
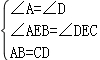 ,
,
∴△ABE≌△DCE(AAS);
(2)∵△ABE≌△DCE,
∴BE=CE,
又∵∠AEB=70°,
∴∠BEC=180°﹣∠AEB=180°﹣70°=110°,
∴∠EBC=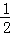 (180°﹣∠BEC)=
(180°﹣∠BEC)=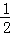 (180°﹣110°)=35°.
(180°﹣110°)=35°.
【点评】本题考查了全等三角形的判定与性质,等腰三角形两底角相等的性质,是基础题,熟练掌握三角形全等的判断方法是解题的关键.


 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
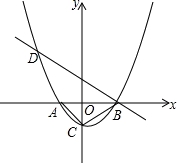
如图,已知抛物线y=m(x+1)(x﹣2)(m为常数,且m>0)与x轴从左至右依次交于A、B两点,与y轴交于点C,且OA=OC,经过点B的直线与抛物线的另一交点D在第二象限.
(1)求抛物线的函数表达式.
(2)在第一象限内的抛物线上是否存在点P,使得以A、B、P为顶点的三角形与△ABC相似?若存在,求出点P的坐标;若不存在,请说明理由.
(3)若∠DBA=30°,设F为线段BD上一点(不含端点),连接AF,一动点M从点A出发,沿线段AF以每秒1个单位的速度运动到F,再沿线段FD以每秒2个单位的速度运动到D后停止,当点F的坐标是多少时,点M在整个运动过程中用时最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
下列说法正确的有( )
(1)两个无理数的和还是无理数;
(2)平方根和立方根都等于本身的数是0和1;
(3)﹣a一定没有算术平方根;
(4)实数有数轴上的点是一一对应的.
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
已知,直线m与y的交点在x轴下方,与x轴距离2个单位长度,且直线m过点(1,﹣1).
(1)求:直线m的表达式;
(2)求:直线m与x轴的交点坐标;
(3)若直线n与直线m在x轴交于同一点,且直线n与直线m以及y轴所围成的三角形面积为4,请直接写出直线n的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com