
 如图,在矩形ABCD中,AB=4,BC=6,将矩形ABCD绕B逆时针旋转30°后得到矩形GBEF,延长DA交FG于点H,则GH的长为( )
如图,在矩形ABCD中,AB=4,BC=6,将矩形ABCD绕B逆时针旋转30°后得到矩形GBEF,延长DA交FG于点H,则GH的长为( )| A. | 8-4$\sqrt{3}$ | B. | $\frac{8\sqrt{3}}{3}$-4 | C. | 3$\sqrt{3}$-4 | D. | 6-3$\sqrt{3}$ |
分析 作辅助线,构建直角△AHM,先由旋转得BG的长,根据旋转角为30°得∠GBA=30°,利用30°角的三角函数可得GM和BM的长,由此得AM和HM的长,相减可得结论.
解答 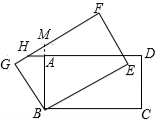 解:如图,延长BA交GF于M,
解:如图,延长BA交GF于M,
由旋转得:∠GBA=30°,∠G=∠BAD=90°,BG=AB=4,
∴∠BMG=60°,
tan∠30°=$\frac{GM}{BG}$=$\frac{\sqrt{3}}{3}$,
∴$\frac{GM}{4}=\frac{\sqrt{3}}{3}$,
∴GM=$\frac{4\sqrt{3}}{3}$,
∴BM=$\frac{8\sqrt{3}}{3}$,
∴AM=$\frac{8\sqrt{3}}{3}$-4,
Rt△HAM中,∠AHM=30°,
∴HM=2AM=$\frac{16\sqrt{3}}{3}$-8,
∴GH=GM-HM=$\frac{4\sqrt{3}}{3}$-($\frac{16\sqrt{3}}{3}$-8)=8-4$\sqrt{3}$,
故选A.
点评 本题考查了矩形的性质、旋转的性质、特殊角的三角函数及直角三角形30°的性质,熟练掌握直角三角形30°所对的直角边等于斜边的一半及特殊角的三角函数值,属于基础题.


科目:初中数学 来源: 题型:选择题
| A. | y=-2x | B. | y=-$\sqrt{3}$x | C. | y=-$\frac{\sqrt{3}}{2}$x | D. | y=2x |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
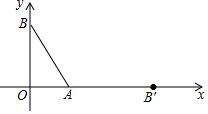 如图,在平面直角坐标系中,点A,B的坐标分别是A(3,0),B(0,4),把线段AB绕点A旋转后得到线段AB′,使点B的对应点B′落在x轴的正半轴上,则点B′的坐标是( )
如图,在平面直角坐标系中,点A,B的坐标分别是A(3,0),B(0,4),把线段AB绕点A旋转后得到线段AB′,使点B的对应点B′落在x轴的正半轴上,则点B′的坐标是( )| A. | (5,0) | B. | (8,0) | C. | (0,5) | D. | (0,8) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 小强从如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:
小强从如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com