
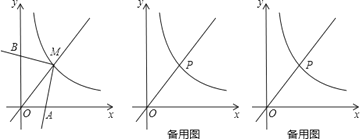
【题目】如图,反比例函数y=![]() (x>0)的图象与直线y=x交于点M,∠AMB=90°,其两边分别与两坐标轴的正半轴交于点A,B,四边形OAMB的面积为6.
(x>0)的图象与直线y=x交于点M,∠AMB=90°,其两边分别与两坐标轴的正半轴交于点A,B,四边形OAMB的面积为6.
(1)求k的值;
(2)点P在反比例函数y=![]() (x>0)的图象上,若点P的横坐标为3,∠EPF=90°,其两边分别与x轴的正半轴,直线y=x交于点E,F,问是否存在点E,使得PE=PF?若存在,求出点E的坐标;若不存在,请说明理由.
(x>0)的图象上,若点P的横坐标为3,∠EPF=90°,其两边分别与x轴的正半轴,直线y=x交于点E,F,问是否存在点E,使得PE=PF?若存在,求出点E的坐标;若不存在,请说明理由.
【答案】(1)6;(2)E(4,0);E(6,0).
【解析】试题分析:(1)过点M作MC⊥x轴于点C,MD⊥y轴于点D,根据AAS证明△AMC≌△BMD,那么S四边形OCMD=S四边形OAMB=6,根据反比例函数比例系数k的几何意义得出k=6;
(2)先根据反比例函数图象上点的坐标特征求得点P的坐标为(3,2).再分两种情况进行讨论:①如图2,过点P作PG⊥x轴于点G,过点F作FH⊥PG于点H,交y轴于点K.根据AAS证明△PGE≌△FHP,进而求出E点坐标;②如图3,同理求出E点坐标.
试题解析:(1)如图1,过点M作MC⊥x轴于点C,MD⊥y轴于点D,

则∠MCA=∠MDB=90°,∠AMC=∠BMD,MC=MD,
∴△AMC≌△BMD,
∴S四边形OCMD=S四边形OAMB=6,
∴k=6;
(2)存在点E,使得PE=PF.
由题意,得点P的坐标为(3,2).
①如图2,过点P作PG⊥x轴于点G,过点F作FH⊥PG于点H,交y轴于点K.
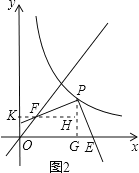
∵∠PGE=∠FHP=90°,∠EPG=∠PFH,PE=PF,
∴△PGE≌△FHP,
∴PG=FH=2,FK=OK=3-2=1,GE=HP=2-1=1,
∴OE=OG+GE=3+1=4,
∴E(4,0);
②如图3,过点P作PG⊥x轴于点G,过点F作FH⊥PG于点H,交y轴于点K.

∵∠PGE=∠FHP=90°,∠EPG=∠PFH,PE=PF,
∴△PGE≌△FHP,
∴PG=FH=2,FK=OK=3+2=5,GE=HP=5-2=3,
∴OE=OG+GE=3+3=6,
∴E(6,0).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】由四舍五入法得到的近似数6.8×103,下列说法中正确的是( )
A.精确到十分位,有2个有效数字 B.精确到个位,有2个有效数字
C.精确到百位,有2个有效数字 D.精确到千位,有4个有效数字
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】受“减少税收,适当补贴”政策的影响,某市居民购房热情大幅提高.据调查,2016年1月该市宏鑫房地产公司的住房销售量为100套,3月份的住房销售量为169套.假设该公司这两个月住房销售量的增长率为x,根据题意所列方程为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
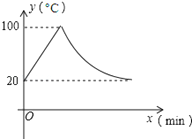
【题目】)我校的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至20℃时自动开机加热,重复上述自动程序.若在水温为20℃时,接通电源后,水温y(℃)和时间(min)的关系如图,
(1) 分别求出直线及双曲线的解析式.
(2)求饮水机接通电源到下一次开机的间隔时间.
(3)在(2)中的时间段内,要想喝到超过50℃的水,有多长时间?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com