
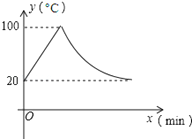
【题目】)我校的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至20℃时自动开机加热,重复上述自动程序.若在水温为20℃时,接通电源后,水温y(℃)和时间(min)的关系如图,
(1) 分别求出直线及双曲线的解析式.
(2)求饮水机接通电源到下一次开机的间隔时间.
(3)在(2)中的时间段内,要想喝到超过50℃的水,有多长时间?
【答案】(1)y=10x+20(0≤x≤8),y=![]() ,(2)40分钟;(3)13分钟.
,(2)40分钟;(3)13分钟.
【解析】试题解析:(1)易得直线过(0,20),(8,100)两点;双曲线过点(8,100),从而求得两个函数的解析式,
(2)代入两个函数y=20求得两个时间相减即可确定答案;
(3)代入两个函数y=50求得两个时间相减即可确定答案.
试题解析:∵开机加热时每分钟上升10℃,
∴从20℃到100℃需要8分钟,
设一次函数关系式为:y=k1x+b,
将(0,20),(8,100)代入y=k1x+b,得k1=10,b=20.
∴y=10x+20(0≤x≤8),
设反比例函数关系式为:y=![]() ,
,
将(8,100)代入,得k=800,
∴y=![]() ,
,
将y=20代入y=![]() ,解得x=40;
,解得x=40;
∴饮水机接通电源到下一次开机的间隔时间为40分钟;
(2)y=10x+20(0≤x≤8)中,
令y=50,解得x=3;
反比例函数y=![]() 中,令y=50,解得:x=16,
中,令y=50,解得:x=16,
∴要想喝到超过50℃的水,有16-3=13分钟.


科目:初中数学 来源: 题型:
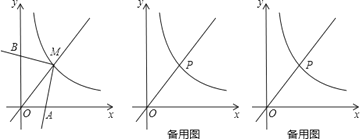
【题目】如图,反比例函数y=![]() (x>0)的图象与直线y=x交于点M,∠AMB=90°,其两边分别与两坐标轴的正半轴交于点A,B,四边形OAMB的面积为6.
(x>0)的图象与直线y=x交于点M,∠AMB=90°,其两边分别与两坐标轴的正半轴交于点A,B,四边形OAMB的面积为6.
(1)求k的值;
(2)点P在反比例函数y=![]() (x>0)的图象上,若点P的横坐标为3,∠EPF=90°,其两边分别与x轴的正半轴,直线y=x交于点E,F,问是否存在点E,使得PE=PF?若存在,求出点E的坐标;若不存在,请说明理由.
(x>0)的图象上,若点P的横坐标为3,∠EPF=90°,其两边分别与x轴的正半轴,直线y=x交于点E,F,问是否存在点E,使得PE=PF?若存在,求出点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长城是我国第一批成功入选世界文化遗产的古迹之一,它的总长经过“四舍五入”精确到十万位的近似数约为6700000米,将6700000用科学记数法表示为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们用字母a表示一个有理数,试判断下列说法是否正确,若不正确,请举出反例.
(1)a一定表示正数,-a一定表示负数;
(2)如果a是零,那么-a就是负数;
(3)若-a是正数,则a一定为非正数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于抛物线y=-(x+1)2+3,下列结论正确的是( )
A. 抛物线的开口向上 B. x≤0时,y随x的增大而减小
C. 顶点坐标为(-1,3) D. 对称轴为直线x=1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com