

���� ��1�����ݡ�ABC�����S=S��IAB+S��IBC+S��IAC���м��㣬���ɵó�r=$\frac{2S}{a+b+c}$��
��2�����ݡ�ABC�����S=$\frac{ab}{2}$����ABC�����S=$\frac{1}{2}��a+b+c��r$�����ɵõ�$\frac{ab}{2}$=$\frac{1}{2}��a+b+c��r$�������ó�$r=\frac{ab}{a+b+c}$���ٸ����ı���IPCQΪ�����Σ����ɵó�$r=\frac{a+b-c}{2}$��������$\frac{ab}{a+b+c}$=$\frac{a+b-c}{2}$���б��Σ��õ�ֱ���������У�a��b��c�Ĺ�ϵΪ��a2+b2=c2��
��� 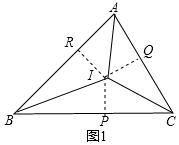 �⣺��1����ͼ1���ߡ�ABC�����߳�AB=c��AC=b��BC=a��IR��AB��IP��BC��IQ��AC��
�⣺��1����ͼ1���ߡ�ABC�����߳�AB=c��AC=b��BC=a��IR��AB��IP��BC��IQ��AC��
���ABC�����S=S��IAB+S��IBC+S��IAC=$\frac{1}{2}$cr+$\frac{1}{2}$ar+$\frac{1}{2}$br=$\frac{1}{2}��a+b+c��r$��
��r=$\frac{2S}{a+b+c}$��
�ʴ�Ϊ��$\frac{1}{2}��a+b+c��r$��$\frac{2S}{a+b+c}$��
��2����ͼ2������Rt��ABC�У���ACB=90�㣬
���ABC�����S=$\frac{ab}{2}$��
�ɣ�1����֪����ABC�����S=$\frac{1}{2}��a+b+c��r$��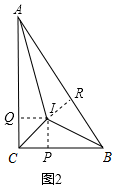
��$\frac{ab}{2}$=$\frac{1}{2}��a+b+c��r$��
��$r=\frac{ab}{a+b+c}$����
�ߡ�IQC=��QCP=��CPI=90�㣬
���ı���CPIQ�Ǿ��Σ�
�֡�IQ=IP��
���ı���IPCQΪ�����Σ�
��CP=CQ=r��
��AQ=b-r��BP=a-r��
�֡�AB=AR+BR=AQ+BP��
��c=b-r+a-r��
��$r=\frac{a+b-c}{2}$����
�ɢ٢ڿɵã�$\frac{ab}{a+b+c}$=$\frac{a+b-c}{2}$��
�ࣨa+b+c����a+b-c��=2ab��
�ࣨa+b��2-c2=2ab��
��a2+2ab+b2-c2=2ab��
��ֱ���������У�a��b��c�Ĺ�ϵΪ��a2+b2=c2��
�ʴ�Ϊ��$\frac{ab}{a+b+c}$��$\frac{a+b-c}{2}$��
���� ���������������ۺ��⣬��Ҫ�����������ε�������㣬�����ε��ж������ʵ����ã��������Ĺؼ�����������������Ƶ����㣮����ڣ�2����ʱע�⣺ֱ�������ε�������ȿ������ù�ʽ���м��㣬Ҳ�������ø�����м��㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
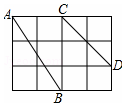 ��ͼ����4��3�����������У�ÿ��С�����εı߳�����1
��ͼ����4��3�����������У�ÿ��С�����εı߳�����1�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2016-2017ѧ�걱�������������꼶��ѧ����ĩ������ѧ�Ծ��������棩 ���ͣ���ѡ��
���������У���ȷ���ǣ� ��
A. 4x+3y=7xy B. 3x2+2=5x2
C. 6xy-4xy=2xy D. 5x2-x2=4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ͬ�ţ��Ҿ�Ϊ���� | B�� | ��� | C�� | ͬ�ţ��Ҿ�Ϊ���� | D�� | ͬ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����10�� | B�� | ����100�� | C�� | ��С10�� | D�� | ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��b��c��d | B�� | b��c��d��a | C�� | c��d��a��b | D�� | c��d��b��a |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com