
 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB,AD⊥CD,垂足为D,AD交⊙O于点E,连接CE.
如图,AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB,AD⊥CD,垂足为D,AD交⊙O于点E,连接CE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
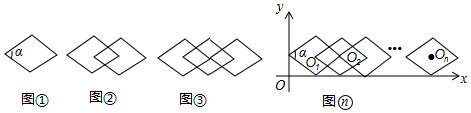
| 图形名称 | 基本图形的个数 | 菱形的个数 |
| 图① | 1 | 1 |
| 图② | 2 | 3 |
| 图③ | 3 | 7 |
| 图④ | 4 | 11 |
| … | … | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 从一副扑克牌中取出方块3、红心6、黑挑10共三张牌,洗匀后正面朝下放在桌面上,小明和小丽玩摸牌游戏,游戏规则如下:先由小明随机摸出一张牌,记下牌面数字后放回,洗匀后正面朝下,再由小丽随机摸出一张牌,记下牌面数字、这样记为一次游戏.当两人摸出的牌面数字不同时,牌面数字大的获胜;当两人摸出的牌面数字相同,则为平局.
从一副扑克牌中取出方块3、红心6、黑挑10共三张牌,洗匀后正面朝下放在桌面上,小明和小丽玩摸牌游戏,游戏规则如下:先由小明随机摸出一张牌,记下牌面数字后放回,洗匀后正面朝下,再由小丽随机摸出一张牌,记下牌面数字、这样记为一次游戏.当两人摸出的牌面数字不同时,牌面数字大的获胜;当两人摸出的牌面数字相同,则为平局.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com