
 (AB+OC)×BO=
(AB+OC)×BO= ×(3+1)×2=4;
×(3+1)×2=4; ×OB×OC═
×OB×OC═ ×2×1=1;
×2×1=1; ×(3+1)×2=4;
×(3+1)×2=4; OB×OC=
OB×OC= ×2×1=1;
×2×1=1;

 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
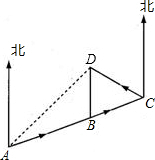 一列火车由A市途经B、C两市到达D市.如图,其中A、B、C三市在同一直线上,D市在A市的北偏东45°方向,在B市的正北方向,在C市的北偏西60°方向,C市在A市的北偏东75°方向.已知B、D两市相距100km.问该火车从A市到D市共行驶了多少路程?(参考数据:
一列火车由A市途经B、C两市到达D市.如图,其中A、B、C三市在同一直线上,D市在A市的北偏东45°方向,在B市的正北方向,在C市的北偏西60°方向,C市在A市的北偏东75°方向.已知B、D两市相距100km.问该火车从A市到D市共行驶了多少路程?(参考数据:| 2 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com