
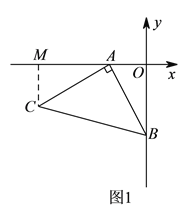
【题目】如图![]() ,
, ![]() ,
, ![]() ,以
,以![]() 点为顶点、
点为顶点、![]() 为腰在第三象限作等腰
为腰在第三象限作等腰![]() .
.
(![]() )求
)求![]() 点的坐标.
点的坐标.
(![]() )如图
)如图![]() ,
, ![]() 为
为![]() 轴负半轴上一个动点,当
轴负半轴上一个动点,当![]() 点沿
点沿![]() 轴负半轴向下运动时,以
轴负半轴向下运动时,以![]() 为顶点,
为顶点, ![]() 为腰作等腰
为腰作等腰![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() 点,求
点,求![]() 的值.
的值.


【答案】(1)点![]() 的坐标为
的坐标为![]() ;(2)
;(2)![]()
【解析】试题分析:(1)如图1,过C作CM⊥x轴于M点,则可以求出△MAC≌△OBA,可得CM=OA=2,MA=OB=4,即可得到结论;
(2)如图2,过D作DQ⊥OP于Q点,则DE=OQ,利用三角形全等的判定定理可得△AOP≌△PQD,进一步可得PQ=OA=2,即OP-DE=2.
试题解析:解:(1)如图1,过C作CM⊥x轴于M点.
∵∠MAC+∠OAB=90°,∠OAB+∠OBA=90°,∴∠MAC=∠OBA.
在△MAC和△OBA中,∵∠CMA=∠AOB=90°,∠MAC=∠OBA,AC=AB,
∴△MAC≌△OBA(AAS),∴CM=OA=2,MA=OB=4,∴OM=OA+AM=2+4=6,∴点C的坐标为(-6,-2).
(2)如图2,过D作DQ⊥OP于Q点,则DE=OQ,∴OP-DE=OP-OQ=PQ.
∵∠APO+∠QPD=90°,∠APO+∠OAP=90°,∴∠QPD=∠OAP.
在△AOP和△PQD中,∵∠AOP=∠PQD=90°,∠OAP=∠QPD,AP=PD,∴△AOP≌△PQD(AAS),∴PQ=OA=2,即OP-DE=2.



科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,连接BD,点E,F分别在AB和CD上,连接CE,AF,CE与AF分别交B于点N,M.已知∠AMD=∠BNC.

(1)若∠ECD=60°,求∠AFC的度数;
(2)若∠ECD=∠BAF,试判断∠ABD与∠BDC之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下面对话,可知懒羊羊所买的笔和笔记本的;
价格分别为( )
喜羊羊:懒羊羊,你上周买的笔和笔记本的价格是多少啊?
懒羊羊:哦,我忘了,只记得先后买了两次,第一次买了5支笔和10本笔记本共花了42元钱,第二次买了10支笔和5本笔记本共花了30元钱。
A. 0.8元/支,2.6元/本 B. 0.8元/支,3.6元/本
C. 1.2元/支,3.6元/本 D. 1.6元/支,3.2元/本
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级同学到距学校6千米的郊外秋游,一部分同学步行,另一部分同学骑自行车,沿相同路线前往,如图,L1L2分别表示步行和骑车的同学前往目的地所走的路程y(千米)与所用时间x(分钟)之间的函数关系,则以下判断错误的是( )

A. 骑车的同学比步行的同学晚出发30分钟
B. 骑车的同学和步行的同学同时到达目的地
C. 骑车的同学从出发到追上步行的同学用了20分钟
D. 步行的速度是6千米/小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,MN是⊙O的直径,MN=4,∠AMN=40°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为( )
A.2
B.2 ![]()
C.2 ![]()
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() 是
是![]() 边的中点,作射线
边的中点,作射线![]() ,与边
,与边![]() 交于点
交于点![]() ,射线
,射线![]() 与直线
与直线![]() 交于点
交于点![]() ,且满足
,且满足![]() .
.
(![]() )如图
)如图![]() ,求证:
,求证: ![]() .
.
(![]() )在点
)在点![]() 运动的过程中,直接写出
运动的过程中,直接写出![]() ,
, ![]() ,
, ![]() 之间的数量关系.
之间的数量关系.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,对角线AC、BD相交于点O,将△COD绕点O按逆时针方向旋转得到△C1OD1 , 旋转角为θ(0°<θ<90°),连接AC1、BD1 , AC1与BD1交于点P.
(1)如图1,若四边形ABCD是正方形.
①求证:△AOC1≌△BOD1 .
②请直接写出AC1 与BD1的位置关系.
(2)如图2,若四边形ABCD是菱形,AC=5,BD=7,设AC1=kBD1 . 判断AC1与BD1的位置关系,说明理由,并求出k的值.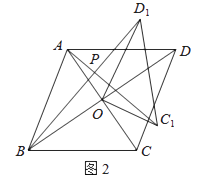
(3)如图3,若四边形ABCD是平行四边形,AC=5,BD=10,连接DD1 , 设AC1=kBD1 . 请直接写出k的值和AC12+(kDD1)2的值.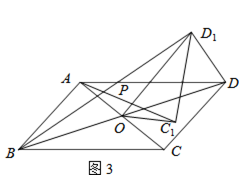
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道对于一个图形,通过不同的方法计算图形的面积可以得到一个数学等式.
例如:由图1可得到(a+b)=a+2ab+b.
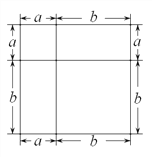
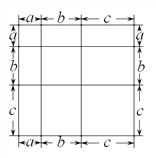
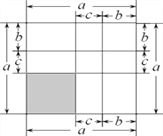
图1 图2 图3
(1)写出由图2所表示的数学等式:_____________________;写出由图3所表示的数学等式:_____________________;
(2)利用上述结论,解决下面问题:已知a+b+c=11,bc+ac+ab=38,求a+b+c的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com