
 在Rt△ABC中,∠ACB=90°,CD是△ABC的高,E是AC的中点,ED、CB的延长线相交于点F,则图中相似三角形有( )
在Rt△ABC中,∠ACB=90°,CD是△ABC的高,E是AC的中点,ED、CB的延长线相交于点F,则图中相似三角形有( )| A. | 3对 | B. | 4对 | C. | 5对 | D. | 6对 |
分析 先用直角三角形的性质结合同角的余角相等,再根据两角对应相等,两三角形相似判断.
解答  解:∵CD是△ABC的高,
解:∵CD是△ABC的高,
∴CD⊥AB,
∴∠ADC=∠BDC=90°,
∴∠CAD+∠ACD=90°,
∵∠ACD+∠BCD=90°,
∴∠CAD=∠BCD,
∵∠ADC=∠BDC,
∴△ACD∽△CBD①,
∵∠A=∠A,∠ACB=∠ADC,
∴△ACB∽△ADC②,
同理:△ACB∽△CBD③,
∵CD⊥AB,
∴∠ADC=∠BDC=90°,
∵E为AC的中点,
∴AE=DE,
∴∠A=∠ADE,
∵∠ADE=∠FDB,
∴∠A=∠FDB,
∵∠ADC=∠ACB=90°,
∴∠A+∠ACD=90°,∠ACD+∠BCD=90°,
∴∠A=∠BCD=∠FDB,
∵∠F=∠F,
∴△FDB∽△FCD④;
共四对,
故选B.
点评 此题是相似三角形的判定,主要考查了相似三角形的判断,同角的余角相等,直角三角形的性质,三角形的高,解本题的关键是判断出△FDB∽△FCD.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)写出两个负数,使它们的差为-5,并写出具体算式.
(1)写出两个负数,使它们的差为-5,并写出具体算式.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
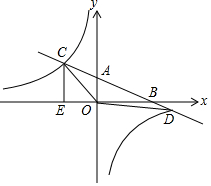 直线AB分别与x轴、y轴交于B和A,与反比例函数的图象交于C、D,CE⊥x轴于点E,tan∠ABO=0.5,OB=4,OE=2.
直线AB分别与x轴、y轴交于B和A,与反比例函数的图象交于C、D,CE⊥x轴于点E,tan∠ABO=0.5,OB=4,OE=2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,是2016年11月月历:
如图,是2016年11月月历:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com