
【题目】已知△ABC的面积是60,请完成下列问题:
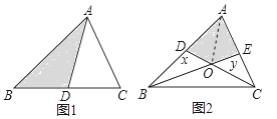
(1)如图1,若AD是△ABC的BC边上的中线,则△ABD的面积________△ACD的面积(填“>”“<”或“=”)
(2)如图2,若CD、BE分别是△ABC的AB、AC边上的中线,求四边形ADOE的面积可以用如下方法:连接AO,由AD=DB得:S△ADO=S△BDO , 同理:S△CEO=S△AEO , 设S△ADO=x,S△CEO=y,则S△BDO=x,S△AEO=y由题意得:S△ABE=![]() S△ABC=30,S△ADC=
S△ABC=30,S△ADC=![]() S△ABC=30,可列方程组为:
S△ABC=30,可列方程组为: ![]() , 解得
, 解得![]() ,通过解这个方程组可得四边形ADOE的面积为________ .
,通过解这个方程组可得四边形ADOE的面积为________ .
科目:初中数学 来源: 题型:
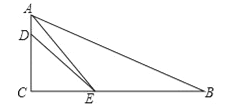
【题目】已知如图,在Rt△ABC中,∠ACB=90°,AE平分∠BAC交BC于点E,D为AC上的点,BE=DE.
(1)求证:∠B+∠EDA=180°;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=6,BC=8,点O在AC上,OA=2,以OA为半径的⊙O交AB于点D,AC于G,BD的垂直平分线交BC于点E,交BD于点F,连接DE.

(1)求证:直线DE是⊙O的切线;
(2)求线段DE的长;
(3)求线段AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)从A地到B地,某甲走直径AB上方的半圆途径;乙先走直径AC上方半圆的途径,再走直径CB下方半圆的途径,如图1,已知AB=40米,AC=30米,计算个人所走的路程,并比较两人所走路程的远近;
(2)如果甲.乙走的路程图改成图2,两人走的路程远近相同吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】瑞士数学家欧拉是史上最伟大的四个数学家之一,目前在百度上搜索关键词“欧拉”,显示的搜索结果约为12 600 000条.将12 600 000用科学记数法表示应为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:①BE=2AE;②△DFP∽△BPH;③△PFD∽△PDB;④DP2=PHPC
其中正确的是( )

A. ①②③④ B. ②③ C. ①②④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为矩形ABCD内的一点,满足OD=OC,若O点到边AB的距离为d,到边DC的距离为3d,且OB=2d,求该矩形对角线的长________

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com