
【题目】如图,在△ABC中,∠C=90°,BC=5米,AC=12米.M点在线段CA上,从C向A运动,速度为1米/秒;同时N点在线段AB上,从A向B运动,速度为2米/秒.运动时间为t秒.
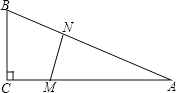
(1)当t为何值时,∠AMN=∠ANM?
(2)当t为何值时,△AMN的面积最大?并求出这个最大值.
【答案】(1)当t为4时,∠AMN=∠ANM.(2)当t=6时,S最大值=![]() 平方米.
平方米.
【解析】
试题分析:(1)用t表示出AM和AN的值,根据AM=AN,得到关于t的方程求得t值即可;
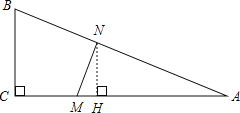
(2)作NH⊥AC于H,证得△ANH∽△ABC,从而得到比例式,然后用t表示出NH,从而计算其面积得到有关t的二次函数求最值即可.
解:(1)∵从C向A运动,速度为1米/秒;同时N点在线段AB上,从A向B运动,速度为2米/秒.运动时间为t秒.
∴AM=12﹣t,AN=2t
∵∠AMN=∠ANM
∴AM=AN,从而12﹣t=2t
解得:t=4 秒,
∴当t为4时,∠AMN=∠ANM.
(2)在Rt△ABC中
∵AB2=BC2+AC2
∴AB=13米
如图,作NH⊥AC于H,
∴∠NHA=∠C=90°,
∵∠A是公共角,
∴△NHA∽△BCA
∴![]() =
=![]() ,
,
即:![]() =
=![]() ,
,
∴NH=![]()
从而有S△AMN=![]() (12﹣t)
(12﹣t)![]() =﹣
=﹣![]() t2+
t2+![]() ,
,
∴当t=6时,S最大值=![]() 平方米.
平方米.


科目:初中数学 来源: 题型:
【题目】给出定义,若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形.
(1)在你学过的特殊四边形中,写出两种勾股四边形的名称;
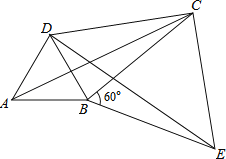
(2)如图,将△ABC绕顶点B按顺时针方向旋转60°得到△DBE,连接AD,DC,CE,已知∠DCB=30°.
①求证:△BCE是等边三角形;
②求证:DC2+BC2=AC2,即四边形ABCD是勾股四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,AD=6cm,CD=8cm,BC=BD=10cm,点P由B出发沿BD方向匀速运动,速度为
1cm/s;同时,线段EF由DC出发沿DA方向匀速运动,速度为1cm/s,交BD于Q,连接PE.若设运动时间为t(s)(0<t<5).解答下列问题:

(1)当t为何值时,PE∥AB?
(2)是否存在某一时刻t,使S△DEQ=![]() ?若存在,求出此时t的值;若不存在,说明理由.
?若存在,求出此时t的值;若不存在,说明理由.
(3)如图2连接PF,在上述运动过程中,五边形PFCDE的面积是否发生变化?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在正方形ABCD中,E为CD的中点,作BE的中垂线GH,垂足为M,则GM:MH的值为( )
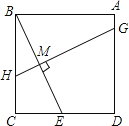
A.4:1 B.3:1 C.3:2 D.5:2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
某车间有32名工人,每人每天可加工甲种零件10个或乙种零件8个。在这32名工人中,一部分工人加工甲种零件,其余的加工乙种零件,已知每加工一个甲种零件可获利35元,每加工一个乙种零件可获利50元。若此车间这一天一共获利12200元,求这一天加工乙种零件工人的人数。
查看答案和解析>>
科目:初中数学 来源: 题型:
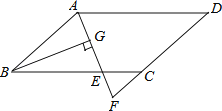
【题目】如图,在ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,BG=![]() ,则△CEF的周长为( )
,则△CEF的周长为( )
A.8 B.9.5 C.10 D.11.5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com