
����Ŀ����ͼ��������ABCD�У�AD��BC��AD=6cm��CD=8cm��BC=BD=10cm����P��B������BD���������˶����ٶ�Ϊ
1cm/s��ͬʱ���߶�EF��DC������DA���������˶����ٶ�Ϊ1cm/s����BD��Q������PE�������˶�ʱ��Ϊt��s����0��t��5��������������⣺

��1����tΪ��ֵʱ��PE��AB��
��2���Ƿ����ijһʱ��t��ʹS��DEQ=![]() �������ڣ������ʱt��ֵ���������ڣ�˵�����ɣ�
�������ڣ������ʱt��ֵ���������ڣ�˵�����ɣ�
��3����ͼ2����PF���������˶������У������PFCDE������Ƿ����仯��˵�����ɣ�
���𰸡���1����t=![]() ��s��ʱ��PE��AB����2����t=2ʱ��S��DEQ=
��s��ʱ��PE��AB����2����t=2ʱ��S��DEQ=![]() ����3�����˶������У������PFCDE��������䣮
����3�����˶������У������PFCDE��������䣮
��������
�����������1����ҪPE��AB����Ӧ��![]() ������t��ʾDE��DP������ʽ���t��ֵ��
������t��ʾDE��DP������ʽ���t��ֵ��
��3������S��DEQ=![]() �������̣����t��ֵ��
�������̣����t��ֵ��
��4������PDE�ա�FBP������S�����PFCDE=S��PDE+S�ı���PFCD=S��FBP+S�ı���PFCD=S��BCD��������ε�������䣮
�⣺��1���������DE=BP=t����DP=10��t��
��PE��AB��
��![]() ��
��
��![]() ��
��
��t=![]() ��
��
����t=![]() ��s��ʱ��PE��AB��
��s��ʱ��PE��AB��
��2�����ڣ�
��DE��BC��
���DEQ�ס�BCD��
��![]() =��
=��![]() ��2��
��2��
��S��DEQ=![]() ��
��
��![]() =��
=��![]() ��2=
��2=![]() ��
��
����![]() ��2=
��2=![]() ��
��
��t2=![]() ��100=4��
��100=4��
t1=2��t2=��2������������ȥ����
����t=2ʱ��S��DEQ=![]() ��
��
��3�����䣮��B��BM��CD����CD��M
��S��BCD=![]() BM=
BM=![]() =8
=8![]() ��
��
����PDE����FBP��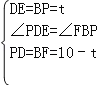 ��
��
���PDE�ա�FBP��
��S�����PFCDE=S��PDE+S�ı���PFCD=S��FBP+S�ı���PFCD=S��BCD=8![]() ��
��
�����˶������У������PFCDE��������䣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����m=2125��n=375����m��n�Ĵ�С��ϵ��ȷ���ǣ� ��
A. m��n B. m��n C. m=n D. ��С��ϵ��ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ƽ��ֱ������ϵ![]() ����ͼ���У�������
����ͼ���У�������![]() ������
������![]() ����
����![]() ����
����![]() ���
���![]() �������������ߵĶԳ���Գƣ�
�������������ߵĶԳ���Գƣ�

��1�����䷽�������������ߵĶ������ꣻ
��2������![]() ��
��![]() ����
����![]() ������ֵ��
������ֵ��
��3����![]() �������������ϵ�һ�����㣬���
�������������ϵ�һ�����㣬���![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() ��
��![]() ��������
��������![]() ��
��![]() ��Ĵ���
��Ĵ���![]() ������Ϊ
������Ϊ![]() �����
�����![]() ����
����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��b��c����ABC�����߳���������|c2��a2��b2|��(a��b)2��0������ABC����״Ϊ____��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���C=90����BC=5�ף�AC=12�ף�M�����߶�CA�ϣ���C��A�˶����ٶ�Ϊ1��/�룻ͬʱN�����߶�AB�ϣ���A��B�˶����ٶ�Ϊ2��/�룮�˶�ʱ��Ϊt�룮
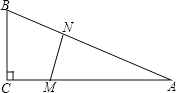
��1����tΪ��ֵʱ����AMN=��ANM��
��2����tΪ��ֵʱ����AMN�����������������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��A��x�������ҵ�A��y��ľ���Ϊ4�����A������Ϊ( )
A. (4��0) B. (0��4) C. (4��0)��(��4��0) D. (0��4)��(0����4)
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com