
【题目】已知在平面直角坐标系![]() (如图)中,抛物线
(如图)中,抛物线![]() 经过点
经过点![]() 、点
、点![]() ,点
,点![]() 与点
与点![]() 关于这条抛物线的对称轴对称;
关于这条抛物线的对称轴对称;

(1)求配方法求这条抛物线的顶点坐标;
(2)联结![]() 、
、![]() ,求
,求![]() 的正弦值;
的正弦值;
(3)点![]() 是这条抛物线上的一个动点,设点
是这条抛物线上的一个动点,设点![]() 的横坐标为
的横坐标为![]() (
(![]() ),过点
),过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,垂足为
,垂足为![]() ,如果
,如果![]() ,求
,求![]() 的值;
的值;
【答案】(1)定点坐标(1,-![]() );(2)
);(2)![]() ;(3)
;(3)![]() 或
或![]() (舍去负
(舍去负
【解析】
试题分析:(1)因A、C在抛物线![]() 上,代入可把抛物线y的解析式求出,通过配方即可得抛物线的顶点坐标.
上,代入可把抛物线y的解析式求出,通过配方即可得抛物线的顶点坐标.
(2)由(1)可知对称轴x=1,且A、B关于x=1对称,可知B(-2,0),AB=6.
又因△ABH为等腰三角形,根据![]() ,所以
,所以![]() ,在Rt△BOC中,BC=
,在Rt△BOC中,BC=![]() ,又因在Rt△BCH中,可求出
,又因在Rt△BCH中,可求出![]() .
.
(3)要求P的横坐标M,就要知道P点构成的Rt△OPQ中的![]() 的值,又因
的值,又因![]() ,故
,故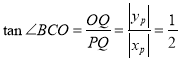 ,在设P
,在设P![]() ,代入抛物线
,代入抛物线![]() ,解得
,解得![]() 或
或![]() (舍去负值).
(舍去负值).
试题解析:(1)代入A(4,0),C(0,-4),得抛物线解析式为![]() ,配方得
,配方得![]() ,
,![]() 顶点坐标为(1,
顶点坐标为(1,![]() ).
).
作![]() 于H,由已知,抛物线对称轴为直线x=1,故B(-2,0),AB=6,由OA=OC=4,则
于H,由已知,抛物线对称轴为直线x=1,故B(-2,0),AB=6,由OA=OC=4,则![]() ,故△ABH为等腰直角三角形.因此BH=AH=
,故△ABH为等腰直角三角形.因此BH=AH=![]() ,又
,又![]() ,故Rt△BCO中,
,故Rt△BCO中,![]() .
.
(3)Rt△BCO中,![]() ,故Rt△OPQ中,
,故Rt△OPQ中, ,故可设
,故可设![]() ,分别代入抛物线解析式
,分别代入抛物线解析式![]() ,解得
,解得![]() 或
或![]() (舍去负值).
(舍去负值).


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
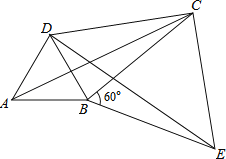
【题目】给出定义,若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形.
(1)在你学过的特殊四边形中,写出两种勾股四边形的名称;
(2)如图,将△ABC绕顶点B按顺时针方向旋转60°得到△DBE,连接AD,DC,CE,已知∠DCB=30°.
①求证:△BCE是等边三角形;
②求证:DC2+BC2=AC2,即四边形ABCD是勾股四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△![]() ,
,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上的延长线上,且
上的延长线上,且![]() (如图);
(如图);
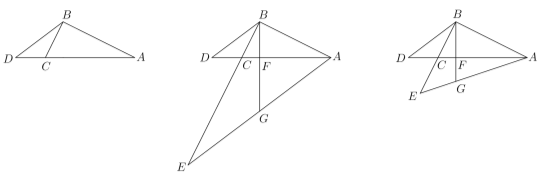
(1)求![]() 的值;
的值;
(2)如果点![]() 在线段
在线段![]() 的延长线上,联结
的延长线上,联结![]() ,过点
,过点![]() 作
作![]() 的垂线,交
的垂线,交![]() 于点
于点![]() ,
,
交![]() 于点
于点![]() ;
;
①如图1,当![]() 时,求
时,求![]() 的值;②如图2,当
的值;②如图2,当![]() 时,求
时,求![]() 的值;
的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,AD=6cm,CD=8cm,BC=BD=10cm,点P由B出发沿BD方向匀速运动,速度为
1cm/s;同时,线段EF由DC出发沿DA方向匀速运动,速度为1cm/s,交BD于Q,连接PE.若设运动时间为t(s)(0<t<5).解答下列问题:

(1)当t为何值时,PE∥AB?
(2)是否存在某一时刻t,使S△DEQ=![]() ?若存在,求出此时t的值;若不存在,说明理由.
?若存在,求出此时t的值;若不存在,说明理由.
(3)如图2连接PF,在上述运动过程中,五边形PFCDE的面积是否发生变化?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
某车间有32名工人,每人每天可加工甲种零件10个或乙种零件8个。在这32名工人中,一部分工人加工甲种零件,其余的加工乙种零件,已知每加工一个甲种零件可获利35元,每加工一个乙种零件可获利50元。若此车间这一天一共获利12200元,求这一天加工乙种零件工人的人数。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com