
【题目】已知:△![]() ,
,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上的延长线上,且
上的延长线上,且![]() (如图);
(如图);
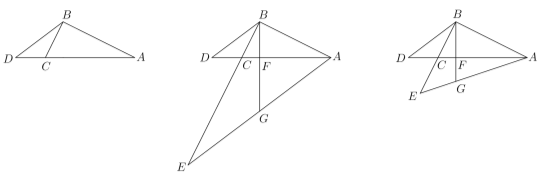
(1)求![]() 的值;
的值;
(2)如果点![]() 在线段
在线段![]() 的延长线上,联结
的延长线上,联结![]() ,过点
,过点![]() 作
作![]() 的垂线,交
的垂线,交![]() 于点
于点![]() ,
,
交![]() 于点
于点![]() ;
;
①如图1,当![]() 时,求
时,求![]() 的值;②如图2,当
的值;②如图2,当![]() 时,求
时,求![]() 的值;
的值;
【答案】(1)![]() (2)①
(2)①![]() ②
②![]()
【解析】
试题分析:(1)因△ABC是Rt△,故![]() ,又因相似三角形的判定定理,可得△DBC∽△DAB,所以有对应线段成比例,故有
,又因相似三角形的判定定理,可得△DBC∽△DAB,所以有对应线段成比例,故有![]() .
.
(2)①要求![]() 的值,就要分别知道BF、FG的值,由题意,延长图形,并根据平行线分线段成比例,可知
的值,就要分别知道BF、FG的值,由题意,延长图形,并根据平行线分线段成比例,可知![]() ,根据射影模型,可知
,根据射影模型,可知![]() ,因此有AF=EH,又因AF//EH,故
,因此有AF=EH,又因AF//EH,故![]() ,再设BF=a,根据线段的关系,可得
,再设BF=a,根据线段的关系,可得![]() .
.
②方法同①.
试题解析:(1)Rt△ABC中,![]() 在△DBC和△DAB中,
在△DBC和△DAB中,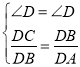 ,故△DBC∽△DAB,因此
,故△DBC∽△DAB,因此![]() ,因此
,因此![]() ,故
,故![]() .
.
(2)①作![]() 交BG的延长线于H,由CF//EH ,则
交BG的延长线于H,由CF//EH ,则![]() ;又由△CFB∽△BFA(射影模型),则
;又由△CFB∽△BFA(射影模型),则![]() ,因此
,因此![]() ,又
,又![]() ,故AF=EH,由AF//EH,故
,故AF=EH,由AF//EH,故![]() .
.
②作![]() 交BG的延长线于H,方法同①,由CF//EH ,则
交BG的延长线于H,方法同①,由CF//EH ,则![]() 且
且![]() ,设CF=a,则AF=4a,EH=2a;
,设CF=a,则AF=4a,EH=2a;![]() 由(1)知
由(1)知![]() ,故DC=
,故DC=![]() ;由AF//EH,故
;由AF//EH,故![]() ,设GH=b,则FG=2b,BF=FH=3b,BG=BF+FG=3b+2b=5b;
,设GH=b,则FG=2b,BF=FH=3b,BG=BF+FG=3b+2b=5b;
因此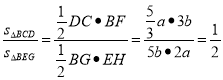 .
.


科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,以AC为底边作等腰△ACD,且使∠ABC=2∠CAD,连接BD.

(1)如图1,若∠ADC=90°,∠BAC=30°,BC=1,求CD的长;
(2)如图1,若∠ADC=90°,证明:AB+BC=![]() BD;
BD;
(3)如图2,若∠ADC=60°,探究AB,BC,BD之间的数量关系并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解方程x2-4x-3=0时,配方后得到的方程为( ).
A.(x+2)2=0 B.(x-2)2=0 C.(x+2)2=2 D.(x-2)2=7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系![]() (如图)中,抛物线
(如图)中,抛物线![]() 经过点
经过点![]() 、点
、点![]() ,点
,点![]() 与点
与点![]() 关于这条抛物线的对称轴对称;
关于这条抛物线的对称轴对称;

(1)求配方法求这条抛物线的顶点坐标;
(2)联结![]() 、
、![]() ,求
,求![]() 的正弦值;
的正弦值;
(3)点![]() 是这条抛物线上的一个动点,设点
是这条抛物线上的一个动点,设点![]() 的横坐标为
的横坐标为![]() (
(![]() ),过点
),过点![]() 作
作![]() 轴的垂线
轴的垂线![]() ,垂足为
,垂足为![]() ,如果
,如果![]() ,求
,求![]() 的值;
的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC的顶点坐标分别是A(0,6),B(-3,-3),C(1,0),将△ABC平移后顶点A的对应点A1的坐标是(4,10),求点B的对应点B1的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com