
【题目】如图,已知△ABC,以AC为底边作等腰△ACD,且使∠ABC=2∠CAD,连接BD.

(1)如图1,若∠ADC=90°,∠BAC=30°,BC=1,求CD的长;
(2)如图1,若∠ADC=90°,证明:AB+BC=![]() BD;
BD;
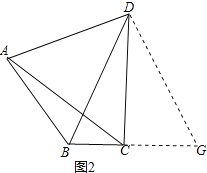
(3)如图2,若∠ADC=60°,探究AB,BC,BD之间的数量关系并证明.
【答案】见解析
【解析】
试题分析:(1)根据等腰直角三角形的性质和已知求出CD的长;
(2)作DE⊥AB于E,DF⊥BC交BC的延长线于F,证明△AED≌△CFD,得到DE=DF,AE=CF,根据正方形的性质证明结论;
(3)延长BC至G,使CG=AB,证明△DAB≌△DCG,得到△DBG是等边三角形,得到答案.
解:(1)∵∠ADC=90°,DA=DC,
∴∠CAD=45°,
∴∠ABC=2∠CAD=90°,又∠BAC=30°,
∴AC=2BC=2,
∴CD=AC×sin∠CAD=![]() ;
;
(2)作DE⊥AB于E,DF⊥BC交BC的延长线于F,
∵∠ADC=90°,DA=DC,
∴∠CAD=45°,
∴∠ABC=2∠CAD=90°,
∴四边形DEBF是矩形,
∵∠ABC=∠ADC=90°,
∴∠BAD+∠BCD=180°,
∴∠BAD=∠FCD,
在△AED和△CFD中,
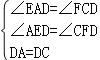 ,
,
∴△AED≌△CFD,
∴DE=DF,AE=CF,
∵四边形DEBF是矩形,DE=DF,
∴四边形DEBF是正方形,
∴BE=BF=![]() BD,又AE=CF,
BD,又AE=CF,
∴AB+BC=BE+BF=![]() BD;
BD;
(3)BD=AB+BC.
延长BC至G,使CG=AB,
∵∠ADC=60°和等腰△ACD,
∴△ACD是等边三角形,
∴∠ABC=2∠CAD=120°,
∴∠BAD+∠BCD=180°,
∴∠BAD=∠GCD,
在△DAB和△DCG中,
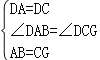 ,
,
∴△DAB≌△DCG,
∴DB=DG,∠CDG=∠ADB,又∠ADB+∠BDC=60°,
∠CDG+∠BDC=60°,
∴△DBG是等边三角形,
∴BD=BG=AB+BC.



 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】2015年10月23日,著名歌手陈奕迅在重庆奥体中心体育馆举办演唱会,歌迷小杨从家出发,乘出租车前往奥体中心观看演出,演唱会结束后,小杨乘坐出租车沿原路返回家,返程时交通拥堵,车流缓慢,若小杨离开家的时间为x(小时),与家的距离为y(千米),则下列各图表示y与x的关系正确的是( )
A.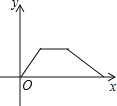 B.
B.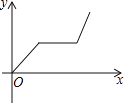
C.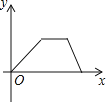 D.
D.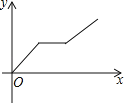
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△![]() ,
,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上的延长线上,且
上的延长线上,且![]() (如图);
(如图);
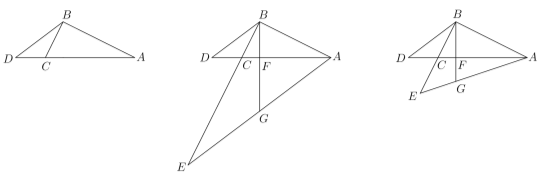
(1)求![]() 的值;
的值;
(2)如果点![]() 在线段
在线段![]() 的延长线上,联结
的延长线上,联结![]() ,过点
,过点![]() 作
作![]() 的垂线,交
的垂线,交![]() 于点
于点![]() ,
,
交![]() 于点
于点![]() ;
;
①如图1,当![]() 时,求
时,求![]() 的值;②如图2,当
的值;②如图2,当![]() 时,求
时,求![]() 的值;
的值;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com