
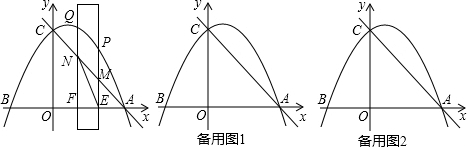
���� ��1�������������ϵ�������������ɽ��ۣ�
��2����ȷ����AF=FN=2��GE=$\frac{\sqrt{2}}{2}$�������ù��ɶ������NE=$\sqrt{5}$�����ɵó����ۣ�
��3����ȷ����ֱ��AC�ĺ�������ʽΪy=-x+5���ٷ�MNΪ�ߺͶԽ����������������������⼴�ɵó����ۣ�
��� �⣺��1����y=0�ã�$-\frac{1}{3}{x^2}+\frac{2}{3}x+5$=0�����x=5��x=-3��
�ߵ�A�ڵ�B���Ҳ࣬
���A��B���������5��0������-3��0����
��x=0ʱ��y=5��
���C��������0��5����
��2����ͼ1����EG��AC������Ϊ��G��
�ߵ�E������Ϊ��4��0����
��OE=4��
��OA=OC=5��
��AE=1����OAC=45�㣮
��AF=FN=2��GE=AE•sin45��=$\frac{\sqrt{2}}{2}$
��Rt��EFN�У����ݹ��ɶ�����֪NE=$\sqrt{E{F}^{2}+F{N}^{2}}$=$\sqrt{5}$��
��sin��ANE=$\frac{GE}{EN}$=$\frac{\frac{\sqrt{2}}{2}}{\sqrt{5}}$=$\frac{\sqrt{10}}{10}$��
��3����ֱ��AC�ĺ�������ʽΪy=kx+b��
����A�͵�C���������ã�$\left\{\begin{array}{l}5k+b=0\\ b=5\end{array}\right.$��
���k=-1��b=5��
��ֱ��AC�ĺ�������ʽΪy=-x+5��
�ٵ�MNΪ��ʱ����ͼ2��ʾ��
���Q��n��$-\frac{1}{3}{n^2}+\frac{2}{3}n+5$����
���P��n+1��$-\frac{1}{3}{n^2}+\frac{16}{3}$������N��n��-n+5��M��n+1��-n+4����
��QN=PM
��$��-\frac{1}{3}{n^2}+\frac{2}{3}n+5��-��-n+5��=��-\frac{1}{3}{n^2}+\frac{16}{3}��-��-n+4��$�����n=2��
���N��������2��3����
�ڵ�MN��ƽ���ı��εĶԽ���ʱ����ͼ3��ʾ��
���F��������m��0����
��N��m��-m+5����M��m+1��-m+4����
Q��m��$-\frac{1}{3}{m^2}+\frac{2}{3}m+5$����P��m+1��$-\frac{1}{3}{m^2}+\frac{16}{3}$����
��QN=PM��
��$��-m+5��-��-\frac{1}{3}{m^2}+\frac{2}{3}m+5��=��-\frac{1}{3}{m^2}+\frac{16}{3}��-��-m+4��$�����m=2��$\sqrt{6}$��
���N��������2+$\sqrt{6}$��3-$\sqrt{6}$����2-$\sqrt{6}$��3+$\sqrt{6}$����
�����������Ե�P��Q��N��MΪ������ı�����ƽ���ı���ʱ����N������Ϊ��2��3��
��2+$\sqrt{6}$��3-$\sqrt{6}$����2-$\sqrt{6}$��3+$\sqrt{6}$����
���� �����Ƕ��κ����ۺ��⣬��Ҫ�����˴���ϵ���������ɶ�����ƽ���ı��ε����ʣ��⣨2���Ĺؼ������NE�ij����⣨3���Ĺؼ��Ƿ�MNΪƽ���ı��εıߺͶԽ�������������÷��̵�˼�������⣬��һ���п������⣮


 �����Ծ���Ԫ���Ծ�ϵ�д�
�����Ծ���Ԫ���Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5 | B�� | 4 | C�� | 3 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
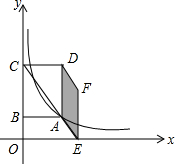 ��ͼ��ʾ����ƽ��ֱ������ϵ�У�����ABCD��BC������y���ϣ��������־��ڵ�һ���ޣ�˫����y=$\frac{k}{x}$����A���ӳ��Խ���CA��x���ڵ�E����AD��AEΪ����ƽ���ı���AEFD����ƽ���ı���AEFD�����Ϊ4����kֵΪ��������
��ͼ��ʾ����ƽ��ֱ������ϵ�У�����ABCD��BC������y���ϣ��������־��ڵ�һ���ޣ�˫����y=$\frac{k}{x}$����A���ӳ��Խ���CA��x���ڵ�E����AD��AEΪ����ƽ���ı���AEFD����ƽ���ı���AEFD�����Ϊ4����kֵΪ��������| A�� | 2 | B�� | 4 | C�� | 8 | D�� | 12 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��2 | B�� | x��2 | C�� | x��2 | D�� | x��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
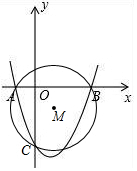 ��ͼ��������y=x2-2x-3��x�ύ��A��-1��0����B��3��0�����㣬��y�ύ�ڵ�C����M��A��B��C���㣬P����������һ�㣬����PA����PA���M����ʱ�����P�����꣮
��ͼ��������y=x2-2x-3��x�ύ��A��-1��0����B��3��0�����㣬��y�ύ�ڵ�C����M��A��B��C���㣬P����������һ�㣬����PA����PA���M����ʱ�����P�����꣮�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com