

分析 (1)先利用等腰三角形的性质得出∠B=30°,再用三角形的外角得出∠BQP=30°,进而得出BP=PQ,即可;
(2)利用三角形的内角和和线段的垂直平分线判断出BP=QP,同(1)的方法即可得出结论;
(3)先找出点M,N的位置,利用锐角三角函数先求出AD,进而得出AA',即可得出结论.
解答 解:(1)∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,当点P和D重合时,∠CPQ=∠B+∠BQP=60°,
∴∠BQP=60°-∠B=30°,
∴BP=QP,
∵AB=AC,AD⊥BC,
∴BD=CD=BP=PC,
∴PQ=PC,
(2)、(1)中结论仍然成立,
理由:如图②,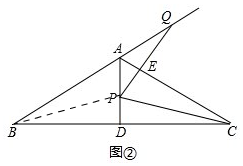
连接BP,∵AB=AC,AD⊥BC,
∴AD是BC的垂直平分线,
∴BP=PC,∠BPD=∠CPD,
∵AB=AC,AD⊥BC,
∴∠DAC=$\frac{1}{2}$∠ABC=60°,
∴∠APQ=180°-∠DAQ-∠BQP=180°-120°-∠BQP=60°-∠BQP,
∵∠APQ+∠CPQ+∠DPC=180°,
∴∠DPC=180°-∠APQ-∠CPQ=180°-(60°-∠BQP)-60°=60°+∠BQP,
∴∠DBP=90°-∠BPD=90°-∠DPC=90°-(60°+∠BQP)=30°-∠BQP,
∵∠DBP+∠PBQ=30°,
∴∠PBQ=30°-∠DBP=30°-(30°-∠BQP)=∠BQP,
∴BP=PC,
∵BP=PC,
∴PQ=PC;
(3)如图,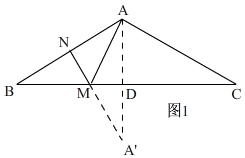
作A关于BC的对称点A',作A'N⊥AB于点N,交BC于点M,则此时AM+MN的最小值,且AM+MN=A'N,
∵AB=AC,∠BAC=120°,
∴∠BAD=60°,
∴∠ABD=30°,BD=$\frac{1}{2}$BC=2,
在Rt△ABD中,AD=BD•tan30°=$\frac{2\sqrt{3}}{3}$,
在Rt△AA'N中,AA'=2AD=$\frac{4\sqrt{3}}{3}$,∠A'AN=60°,
∴A'N=AA'•tan60°=$\frac{4\sqrt{3}}{3}$×$\sqrt{3}$=4,
即:AM+MN的最小值是4.
点评 此题是三角形综合题,主要考查了等腰三角形的性质和判定,三角形的内角和定理,三角形外角的性质,锐角三角函数,解(2)的关键是判断出PB=PQ,解(3)的关键是找出点M,N的位置,是一道中等难度的中考常考题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
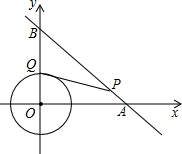 如图,⊙O是以原点为圆心,2$\sqrt{3}$为半径的圆,点P是直线上y=-x+8的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )
如图,⊙O是以原点为圆心,2$\sqrt{3}$为半径的圆,点P是直线上y=-x+8的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )| A. | 4 | B. | 2$\sqrt{5}$ | C. | 8-2$\sqrt{3}$ | D. | 2$\sqrt{13}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
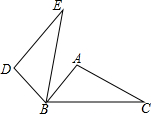 如图,△ABC中,∠ABC=50°,∠C=30°,将△ABC绕点B逆时针旋转α(0°<α≤90°)得到△DBE,若DE∥AB,则α为( )
如图,△ABC中,∠ABC=50°,∠C=30°,将△ABC绕点B逆时针旋转α(0°<α≤90°)得到△DBE,若DE∥AB,则α为( )| A. | 50° | B. | 70° | C. | 80° | D. | 90° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com