练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】菱形具有而矩形不具有的性质是（　　）

    A. 两组对边分别平行 B. 对角线相等

    C. 对角线互相垂直 D. 两组对角分别相等

    【答案】C

    【解析】

    菱形和矩形都是平行四边形，具有平行四边形的所有性质，菱形还具有独特的性质：四边相等，对角线垂直；矩形具有独特的性质：对角线相等，邻边互相垂直．

    解：A、两组对边分别平行，菱形和矩形都具有的性质，故A错误；

    B、对角线相等是矩形具有而菱形不具有的性质，故D错误；

    C、对角线互相垂直，菱形的性质，矩形不具有的性质，故C正确；

    D、两组对角分别相等，菱形和矩形都具有的性质，故B错误；

    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】下列图形中,一定可以拼成平行四边形的是( )
    A.两个等腰三角形
    B.两个直角三角形
    C.两个锐角三角形
    D.两个全等三角形

    查看答案和解析>>

    科目：初中数学 来源： 题型：

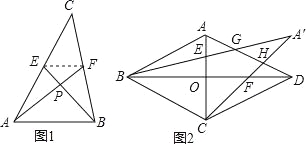
    【题目】(2016湖南省邵阳市第25题)尤秀同学遇到了这样一个问题：如图1所示，已知AF，BE是△ABC的中线，且AF⊥BE，垂足为P，设BC=a，AC=b，AB=c．

    求证：a2+b2=5c2

    该同学仔细分析后，得到如下解题思路：

    先连接EF，利用EF为△ABC的中位线得到△EPF∽△BPA，故，设PF=m，PE=n，用m，n把PA，PB分别表示出来，再在Rt△APE，Rt△BPF中利用勾股定理计算，消去m，n即可得证

    （1）请你根据以上解题思路帮尤秀同学写出证明过程．

    （2）利用题中的结论，解答下列问题：

    在边长为3的菱形ABCD中，O为对角线AC，BD的交点，E， F分别为线段AO，DO的中点，连接BE，CF并延长交于点M，BM，CM分别交AD于点G，H，如图2所示，求MG2+MH2的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】用直尺和圆规作一个角等于已知角的示意图如下，则要说明∠D′O′C′=∠DOC，需要证明△D′O′C′≌△DOC，则这两个三角形全等的依据是__（写出全等的简写）．

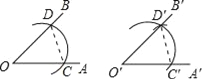
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(2016宁夏第22题)某种型号油电混合动力汽车，从A地到B地燃油行驶纯燃油费用76元，从A地到B地用电行驶纯电费用26元，已知每行驶1千米，纯燃油费用比纯用电费用多0.5元．

    （1）求每行驶1千米纯用电的费用；

    （2）若要使从A地到B地油电混合行驶所需的油、电费用合计不超过39元，则至少用电行驶多少千米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知点P(a+3，2a+4)在x轴上，则点P的坐标为________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】给出下列5种图形：①平行四边形②菱形③正五边形、④正六边形、⑤等腰梯形中，既是轴对称又是中心对称的图形有________个．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知函数y=x+1的图象与y轴交于点A，一次函数y=kx+b的图象经过点B（0，-1），与x轴以及y=x+1的图象分别交于点C、D，且点D的坐标为（1，n），

    （1）点A的坐标是 ，n= ，k= ，b= ；

    （2）x取何值时，函数y=kx+b的函数值大于函数y=x+1的函数值；

    （3）求四边形AOCD的面积；

    （4）是否存在y轴上的点P，使得以点P，B，D为顶点的三角形是等腰三角形？若存在求出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一元二次方程x（x﹣1）=0的解是

    查看答案和解析>>

    同步练习册答案